


Next: Keyboard Instruments
Up: Lectures
Previous: Woodwind Instruments
Percussion instruments come in a wide variety of shapes and forms. One might suggest that any object could be used as a percussion instrument ... just bang on it! The more traditional members, however, can be roughly grouped as idiophones (xylophone, marimba, chimes, cymbals, gongs, etc.), membranophones (drums), aerophones (whistles, sirens), and chordophones (piano, harpsichord).
We will consider only members of the first two groups above in this section. These instruments will typically not produce harmonic overtones, though a few partials can often be ``tuned'' to approximate integer ratios of a fundamental.
- Vibrations of Bars:
- Vibrations in bars are primarily one-dimensional.
- Longitudinal vibrations are harmonic with frequencies
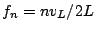 for
for
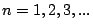 , where
, where
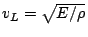 is the speed of sound in the rod,
is the speed of sound in the rod, 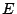 is Young's elastic modulus,
is Young's elastic modulus, 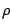 is the density, and
is the density, and 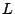 is the length of the rod.
is the length of the rod.
- Longitudinal vibrations are much higher in frequency than transverse vibrations.
- Transverse vibration frequencies for a bar free at both ends are
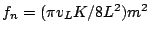 , where
, where 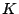 is the radius of gyration (= thickness/3.46 for a flat bar) and
is the radius of gyration (= thickness/3.46 for a flat bar) and
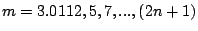 . This results in modal frequency ratios of 1.0 : 2.76 : 5.40 : 8.90, etc.
. This results in modal frequency ratios of 1.0 : 2.76 : 5.40 : 8.90, etc.
- Rectangular Bars (The Glockenspiel):
- The typical range of the glockenspiel is from
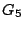 (f = 784 Hz) to
(f = 784 Hz) to 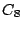 (f = 4186 Hz).
(f = 4186 Hz).
- All but the lowest transverse mode die out quickly when the bar is struck. Thus, we hear a clear ring at the frequency of the fundamental transverse mode.
- The Marimba, Xylophone, and Vibes:
- The bars of the marimba, xylophone, and vibraphone are cut with an arch on their underside. This produces lower pitches for a given length (compared to the uniform bar) and also allows tuning of the partials.
- These instruments are outfitted with tubular resonators under each bar, tuned to the fundamental.
- The second partial of the marimba is tuned to about a two-octave interval (a ratio of 4.0). The third partial has a frequency around 9.2 times the fundamental (about three octaves plus a minor third above).
- The bars of the xylophone are less undercut and the first overtone is tuned to a twelfth (a ratio of 3.0).
- Vibraphones use deeply undercut aluminum bars with the first overtone tuned to a two-octave interval. The metal bars tend to have much longer decay times than the wood or synthetic bars of marimbas and xylophones.
- The most distinctive feature of vibraphones is the vibrato introduced by motor-driven discs at the top of the resonators.
- Chimes:
- Tubular bells are fabricated from lengths of brass tubing. The upper end of each tube is partially or completely closed by a brass plug with a protruding rim.
- The strike tone one hears is based on modes 4, 5, and 6. The frequencies associated with these modes form rough ratios of 2:3:4, and thus cause our auditory system to perceive a fundamental at one octave below the 4th mode (though no such mode exists).
- Vibrations of Plates:
- The restoring force in plates, like bars, results from the stiffness of the solid material.
- The overtones tend to be substantially higher than the fundamental.
- Cymbals:
- Coupling between vibrational modes is very strong in cymbals, so that a large number of partials quickly appear in the spectrum when it is excited.
- Low-frequency energy is converted via a passive nonlinearity to high-frequency energy over several seconds after striking.
- Gongs and Tamtams:
- Gongs are tuned to a definite pitch. When struck near the center with a soft mallet, their sound builds up slowly and continues for quite a while.
- Tamtams do not have the dome of the gong and have much less of a definite pitch.
- Bells and Carillons:
- The strike tone is determined by partials with ratios 2:3:4 (the octave, twelfth, and double-octave), as in the chimes. Unlike chimes, however, the carillon bells have a prime mode at or near the strike tone (though the pitch of the strike tone is apparently more dependent on the upper partials).
- Vibrations of Membranes:
- The vibrations of a membrane are primarily two-dimensional.
- Analytic solutions for various geometries (square, circular, elliptical) are possible and involve the solution of the two-dimensional wave equation.
- For a circular membrane, the modal frequencies are given by
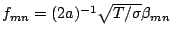 , where
, where 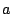 is the radius of the membrane,
is the radius of the membrane, 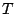 is the tension,
is the tension, 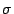 is the area density, and
is the area density, and 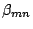 is the
is the 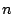 th zero value of the
th zero value of the 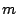 th-order Bessel function.
th-order Bessel function.
- Timpani:
- The mass of the air contained inside the kettle lowers the frequencies of the non-circularly concentric modes [(1,1), (2,1), (3,1), etc.].
- The stiffness of the air contained inside the kettle raises the frequencies of the circularly concentric modes [(0,1), (0,2), (0,3), etc.].
- The circularly concentric modes damp out rather quickly and do not contribute greatly to the timbre of the drum.
- The other modes produce frequencies nearly in the ratios 1 : 1.5 : 2 : 2.5, though a ``missing fundamental'' is not perceived.
- Bass Drum and Snare Drum:
- These drums do not convey a definite pitch.
- The bass drum has many nearly harmonic modes in its low-frequency range, as in the timpani. However, the abundance of louder sounding non-harmonic modes above 200 Hz mask out any sense of pitch.

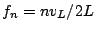 for
for
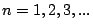 , where
, where
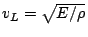 is the speed of sound in the rod,
is the speed of sound in the rod, 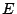 is Young's elastic modulus,
is Young's elastic modulus, 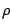 is the density, and
is the density, and 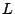 is the length of the rod.
is the length of the rod.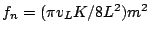 , where
, where 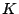 is the radius of gyration (= thickness/3.46 for a flat bar) and
is the radius of gyration (= thickness/3.46 for a flat bar) and
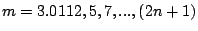 . This results in modal frequency ratios of 1.0 : 2.76 : 5.40 : 8.90, etc.
. This results in modal frequency ratios of 1.0 : 2.76 : 5.40 : 8.90, etc.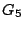 (f = 784 Hz) to
(f = 784 Hz) to 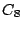 (f = 4186 Hz).
(f = 4186 Hz).

