• Simple Harmonic Motion
• Damping
• The Helmoltz Resonator
• A One-Mass, Two-Spring System
• A Two-Mass, Three-Spring System
• Multiple Mass Systems

Vibrating Systems

Simple Harmonic Motion

1. The Ideal Mass:
   
   
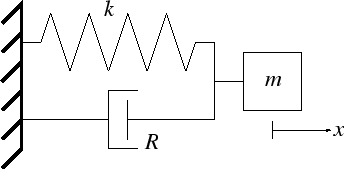
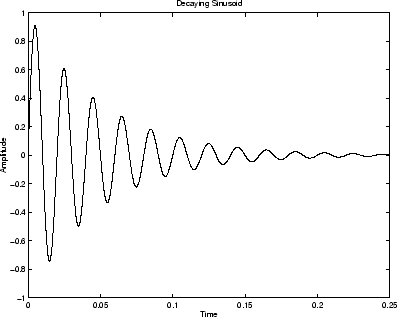
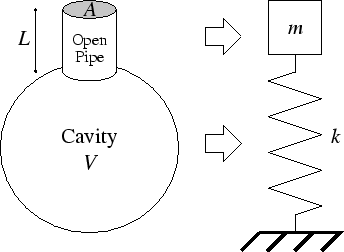
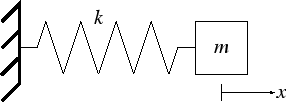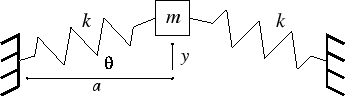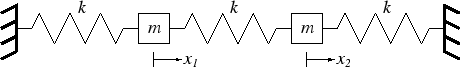   • The motion of an ideal mass is unaffected by friction or any other damping force.
   • The ideal mass is completely rigid.
   • By Newton's Second Law: $F = m a = m \frac{dv}{dt} = m \frac{d^{2}x}{dt^{2}}$

2. The Ideal Spring:
   
   
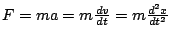
   • The ideal spring has no mass or internal damping.
   • Hooke's Law: $F = -k x$ (valid for small, non-distorting displacements)
   • The spring's equilibrium position is given by $x=0$.
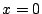   • A positive value of 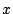$x$ produces a negative restoring force.

3. The Ideal Mass-Spring System:

   Figure 1: An ideal mass-spring system.

   
   • System equation: $m \frac{d^{2}x}{dt^{2}} + k x = 0$
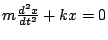
   • This second-order differential equation has solutions of the form $x = A \cos(\omega_{0}t + \phi)$.
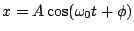   • $\omega_{0} = \sqrt{k/m}$ is the characteristic (or natural) angular frequency of the system.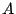
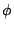   • $A$ and $\phi$ are determined by the initial displacement and velocity.
   • There are no losses in the system, so it will oscillate forever.

4. Energy in the Ideal Mass-Spring System:
   
   
   • The potential energy (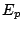$E_{p}$) of the ideal mass-spring system is equal to the work done stretching or compressing the spring: $E_{p} = - \int_{0}^{x}F dx = \int_{0}^{x} k x dx = \frac{1}{2} k x^{2} = \frac{1}{2} k A^{2} \cos^{2}(\omega_{0}t + \phi)$.
   • The kinetic energy (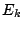$E_{k}$) of the ideal mass-spring system is given by the motion of mass: $E_{k} = \frac{1}{2} m v^{2} = \frac{1}{2} m \omega_{0}^{2} A^{2} \sin^{2}(\omega_{0}t + \phi) = \frac{1}{2} k A^{2} \sin^{2}(\omega_{0}t + \phi)$.
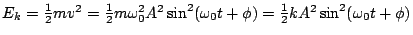   • The total energy of the ideal mass-spring system is constant: $E = E_{p} + E_{k} = \frac{1}{2} k A^{2} = \frac{1}{2} m v_{\mathrm{max}}^{2}$
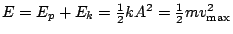
   • At the extremes of its displacement, the mass is at rest and has no kinetic energy. At the same time, the spring is maximally compressed or stretched, and thus stores all the mechanical energy of the system as potential energy.
   • When the mass is in motion and reaches the equilibrium position of the spring, the mechanical energy of the system has been completely converted to kinetic energy.
   • All vibrating systems consist of this interplay between an energy storing component and an energy carrying (``massy'') component.

Damping

1. The Ideal Mechanical Resistance:
   
   
   • Force due to mechanical resistance or viscosity is typically approximated as being proportional to velocity: $F = R v = R \frac{dx}{dt}$

2. The Ideal Mass-Spring-Damper System:

   Figure 2: An ideal mass-spring-damper system.

   
   • System equation: $m \frac{d^{2}x}{dt^{2}} + R \frac{dx}{dt} + k x = 0$
   • This second-order differential equation has solutions of the form $x = e^{-\alpha t} A \cos(\omega_{d}t + \phi)$.

     Figure 3: A decaying sinusoid.

     

   • $\alpha = R/(2m)$ is a decay constant and $\omega_{d} = \sqrt{\omega_{0}^{2} - \alpha^{2}}$ is the characteristic (or natural) angular frequency of the system.
   • $A$ and $\phi$ are determined by the initial displacement and velocity.
   • The natural frequency $\omega_{d}$ is lower than that of the mass-spring system ($\omega_{0}$).

The Helmoltz Resonator

Figure 4: The Helmholtze Resonator and its mechanical correlate.

• In the ``low-frequency limit'', an open tube is a direct acoustic correlate to the mechanical mass.
• In the ``low-frequency limit'', a cavity is a direct acoustic correlate to the mechanical spring.
• Using Newton's Second Law to model the air mass in the tube and Hooke's Law for fluids to model the compressibility of the air cavity, a sinusoidal solution can be found with natural frequency $\omega_{0} = c \sqrt{A/(L V)}$, where $c$ is the speed of sound in air, $A$ is the cross-sectional area of the tube, $L$ is the length of the tube, and $V$ is the volume of the cavity.

A One-Mass, Two-Spring System

1. Longitudinal Motion (along x-axis):

   Figure 5: A one-mass, two-spring system: Longitudinal motion.

   
   • The net restoring force on the mass: $F_{x} = -2 k x$
   • System natural frequency: $\omega_{0} = \sqrt{2 k/m}$

2. Transverse Motion (along y-axis):

   Figure 6: A one-mass, two-spring system: Vertical motion.

   
   • If the springs are initially stretched a great deal from their relaxed length (but not distorted), the vibration frequency is nearly the same as for longitudinal vibrations.
   • If the springs are initially stretched very little from their relaxed length, the ``natural'' frequency is much lower and the vibrations are nonlinear (nonsinusoidal) for all but the smallest of $y$-axis displacements.

A Two-Mass, Three-Spring System

1. Longitudinal Motion (along x-axis):

   Figure 7: A two-mass, three-spring system: Longitudinal motion.

   
   • System equations:
   
   
   $$m \frac{d^{2}x_{1}}{dt^{2}} + k x_{1} + k (x_{1} - x_{2}) = ... ... m \frac{d^{2}x_{2}}{dt^{2}} + k x_{2} + k (x_{2} - x_{1}) = 0$$
   
   
   • Natural frequencies: $\omega = \omega_{0}, \sqrt{3}\omega_{0}$, where $\omega_{0} = \sqrt{k/m}$

Multiple Mass Systems

• Each additional mass adds another natural mode of vibration per axis of motion.
• Analyses of this type are called ``lumped characterizations''.