Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Time Varying OLA Modifications
In the preceding sections, we assumed that the spectral modification
 did not vary over time. We will now examine the implications of
time-varying spectral modifications. The derivation below
follows [9], except that we'll keep our previous
notation:
did not vary over time. We will now examine the implications of
time-varying spectral modifications. The derivation below
follows [9], except that we'll keep our previous
notation:
Using 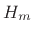 in our OLA formulation with a hop size
in our OLA formulation with a hop size 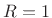 results in
results in
Define
 to get
to get
 |
(9.42) |
Let's examine the term
 in more detail:
in more detail:
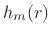 describes the time variation of the
describes the time variation of the  tap.
tap.
-
![$ \sum_{m=-\infty}^\infty h_m(r) w[(n-r)-m] = [h_{(\cdot)}(r) \ast w](n-r)$](img1497.png) is a filtered version of the
is a filtered version of the  tap
tap 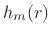 . It is
lowpass-filtered by w and delayed by
. It is
lowpass-filtered by w and delayed by 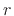 samples.
samples.
- Denote the
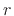 th time-varying, lowpass-filtered, delayed-by-
th time-varying, lowpass-filtered, delayed-by-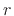 filter tap by
filter tap by
 . This can be interpreted
as the weighting in the output at time
. This can be interpreted
as the weighting in the output at time 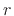 of an impulse entering
the time-varying filter at time
of an impulse entering
the time-varying filter at time  .
.
Using this, we get
This is a superposition sum for an arbitrary linear, time-varying filter
$](img1501.png) .
.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() did not vary over time. We will now examine the implications of
time-varying spectral modifications. The derivation below
follows [9], except that we'll keep our previous
notation:
did not vary over time. We will now examine the implications of
time-varying spectral modifications. The derivation below
follows [9], except that we'll keep our previous
notation:

![]() in our OLA formulation with a hop size
in our OLA formulation with a hop size ![]() results in
results in
![\begin{eqnarray*}
y(n) &=& \sum_{m=-\infty}^\infty y_m(n) \\
&=& \sum_{m=-\infty}^\infty \frac{1}{N}\sum_{k=0}^{N-1} X_m(\omega_k) H_m(\omega_k) e^{j\omega_kn} \\
&=& \sum_{m=-\infty}^\infty \frac{1}{N}\sum_{k=0}^{N-1}
\left[ \sum_{l=-\infty}^\infty x(l) w(l-m)e^{-j\omega_kl} \right]
H_m(\omega_k) e^{j\omega_kn} \\
&=& \sum_{l=-\infty}^\infty x(l) \sum_{m=-\infty}^\infty w(l-m)
\frac{1}{N}\sum_{k=0}^{N-1} H_m(\omega_k)
e^{j\omega_k(n-l)} \\
&=& \sum_{l=-\infty}^\infty x(l)
\sum_{m=-\infty}^\infty w(l-m) h_m(n-l) \\
\end{eqnarray*}](img1491.png)
 to get
to get

 in more detail:
in more detail:
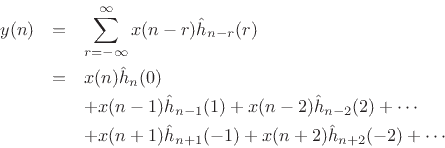
![]() .
.