Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
For each window sample,
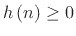 , or,
, or,
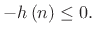 |
(4.66) |
Stacking inequalities for all 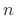 ,
,
![$\displaystyle \left[\begin{array}{ccccc} -1 & 0 & \cdots & 0 & 0\\ 0 & -1 & & & 0\\ \vdots & & \ddots & & \vdots \\ 0 & & & -1 & 0\\ 0 & 0 & \cdots & 0 & -1\end{array} \right]\left[\begin{array}{c} h\left(0\right)\\ h\left(1\right)\\ \vdots \\ h\left(L-1\right)\\ h\left(L\right)\end{array} \right] \le \left[\begin{array}{c} 0\\ 0\\ \vdots \\ 0\\ 0 \end{array} \right]$](img593.png) |
(4.67) |
or
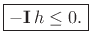 |
(4.68) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() , or,
, or,
![$\displaystyle \left[\begin{array}{ccccc} -1 & 0 & \cdots & 0 & 0\\ 0 & -1 & & & 0\\ \vdots & & \ddots & & \vdots \\ 0 & & & -1 & 0\\ 0 & 0 & \cdots & 0 & -1\end{array} \right]\left[\begin{array}{c} h\left(0\right)\\ h\left(1\right)\\ \vdots \\ h\left(L-1\right)\\ h\left(L\right)\end{array} \right] \le \left[\begin{array}{c} 0\\ 0\\ \vdots \\ 0\\ 0 \end{array} \right]$](img593.png)