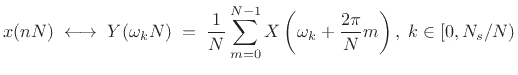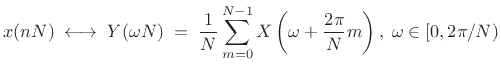Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
To show:
or
From the DFT case [264], we know this is true when 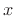 and
and 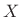 are each complex sequences of length
are each complex sequences of length 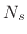 , in which case
, in which case 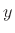 and
and 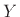 are length
are length 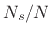 . Thus,
. Thus,
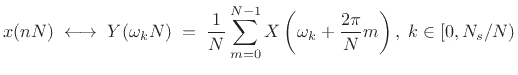 |
(3.38) |
where we have chosen to keep frequency samples  in terms of
the original frequency axis prior to downsampling, i.e.,
in terms of
the original frequency axis prior to downsampling, i.e.,
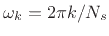 for both
for both 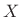 and
and 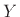 . This choice allows us to easily take
the limit as
. This choice allows us to easily take
the limit as
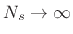 by simply replacing
by simply replacing  by
by 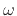 :
:
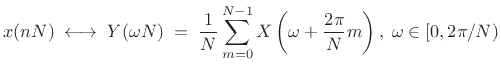 |
(3.39) |
Replacing 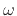 by
by
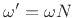 and converting to
and converting to 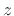 -transform
notation
-transform
notation  instead of Fourier transform notation
instead of Fourier transform notation 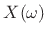 ,
with
,
with
 , yields the final result.
, yields the final result.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
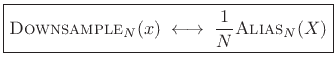
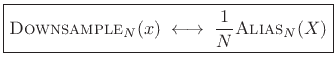
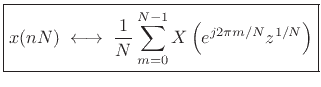
![]() and
and ![]() are each complex sequences of length
are each complex sequences of length ![]() , in which case
, in which case ![]() and
and ![]() are length
are length ![]() . Thus,
. Thus,