The Simplest Lowpass Filter

Let's start with a very basic example of the generic problem at hand: understanding the effect of a digital filter on the spectrum of a digital signal. The purpose of this example is to provide motivation for the general theory discussed in later chapters.

Figure 1.1: Amplitude response (gain versus frequency) specification for the ideal low-pass filter.

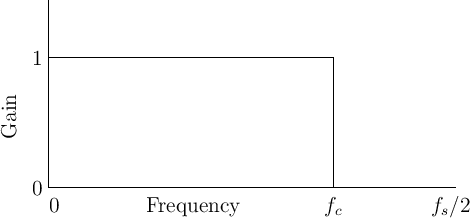
Our example is the simplest possible low-pass filter. A low-pass filter is one which does not affect low frequencies and rejects high frequencies. The function giving the gain of a filter at every frequency is called the amplitude response (or magnitude frequency response). The amplitude response of the ideal lowpass filter is shown in Fig.1.1. Its gain is 1 in the passband, which spans frequencies from 0 Hz to the cut-off frequency $f_c$ Hz, and its gain is 0 in the stopband (all frequencies above $f_c$ ). The output spectrum is obtained by multiplying the input spectrum by the amplitude response of the filter. In this way, signal components are eliminated (``stopped'') at all frequencies above the cut-off frequency, while lower-frequency components are ``passed'' unchanged to the output.