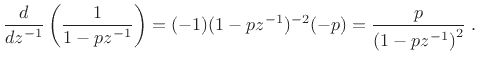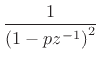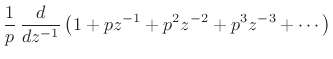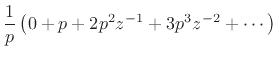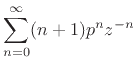Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In the time domain, repeated poles give rise to polynomial
amplitude envelopes on the decaying exponentials corresponding to the
(stable) poles. For example, in the case of a single pole repeated
twice, we have
Proof:
First note that
Therefore,
Note that 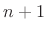 is a first-order polynomial in
is a first-order polynomial in 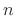 . Similarly, a pole
repeated three times corresponds to an impulse-response component that
is an exponential decay multiplied by a quadratic polynomial in
. Similarly, a pole
repeated three times corresponds to an impulse-response component that
is an exponential decay multiplied by a quadratic polynomial in
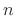 , and so on. As long as
, and so on. As long as 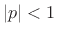 , the impulse response will
eventually decay to zero, because exponential decay always overtakes
polynomial growth in the limit as
, the impulse response will
eventually decay to zero, because exponential decay always overtakes
polynomial growth in the limit as 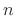 goes to infinity.
goes to infinity.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]