Starting with the defining equation for an eigenvector
![]() and its
corresponding eigenvalue
and its
corresponding eigenvalue ![]() ,
,
we get
Equation (G.23) gives us two equations in two unknowns:
![\begin{eqnarray*}
1+c+c\eta_i &=& [c+\eta_i (c-1)]\eta_i = c\eta_i + \eta_i ^2 (c-1)\\
\,\,\Rightarrow\,\,1+c &=& \eta_i ^2 (c-1)\\
\,\,\Rightarrow\,\,\eta_i &=& \pm \sqrt{\frac{c+1}{c-1}}.
\end{eqnarray*}](img2311.png)
Thus, we have found both eigenvectors
![\begin{eqnarray*}
\underline{e}_1&=&\left[\begin{array}{c} 1 \\ [2pt] \eta \end{array}\right],\qquad
\underline{e}_2=\left[\begin{array}{c} 1 \\ [2pt] -\eta \end{array}\right], \quad \hbox{where}\\
\eta&\isdef &\sqrt{\frac{c+1}{c-1}}.
\end{eqnarray*}](img2312.png)
They are linearly independent provided
![]() and finite provided
and finite provided ![]() .
.
We can now use Eq.(G.24) to find the eigenvalues:
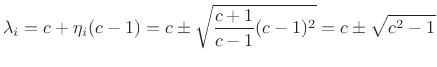
Assuming
Let us henceforth assume
![]() . In this range
. In this range
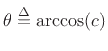 is real, and we have
is real, and we have
![]() ,
,
![]() . Thus, the eigenvalues can be expressed as follows:
. Thus, the eigenvalues can be expressed as follows:
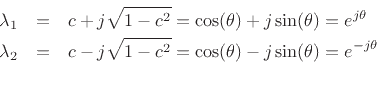
Equating ![]() to
to
![]() , we obtain
, we obtain
![]() , or
, or
![]() , where
, where ![]() denotes the sampling rate. Thus the
relationship between the coefficient
denotes the sampling rate. Thus the
relationship between the coefficient ![]() in the digital waveguide
oscillator and the frequency of sinusoidal oscillation
in the digital waveguide
oscillator and the frequency of sinusoidal oscillation ![]() is
expressed succinctly as
is
expressed succinctly as
We see that the coefficient range (-1,1) corresponds to frequencies in the range
We have now shown that the system of Fig.G.3 oscillates
sinusoidally at any desired digital frequency ![]() rad/sec by simply
setting
rad/sec by simply
setting
![]() , where
, where ![]() denotes the sampling interval.
denotes the sampling interval.