One of the simplest formulations of recursive digital filter design is based on minimizing the equation error. This method allows matching of both spectral phase and magnitude. Equation-error methods can be classified as variations of Prony's method [48]. Equation error minimization is used very often in the field of system identification [46,30,78].
The problem of fitting a digital filter to a given spectrum may be formulated as follows:
Given a continuous complex function
![]() ,
corresponding to a causalI.4 desired
frequency-response, find a stable digital filter of the form
,
corresponding to a causalI.4 desired
frequency-response, find a stable digital filter of the form
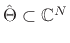
where
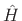
with
![]() given, such that some norm of the error
given, such that some norm of the error
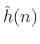
is minimum with respect to the filter coefficients
![$\displaystyle \hat{\theta}^T\isdef \left[\hat{b}_0,\hat{b}_1,\ldots\,,\hat{b}_{{n}_b},\hat{a}_1,\hat{a}_2,\ldots\,,\hat{a}_{{n}_a}\right]^T,
$](img2438.png)
which are constrained to lie in a subset
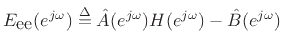 . When explicitly stated, the filter
coefficients may be complex, in which case
. When explicitly stated, the filter
coefficients may be complex, in which case
The approximate filter ![]() is typically constrained to be stable,
and since positive powers of
is typically constrained to be stable,
and since positive powers of ![]() do not appear in
do not appear in
![]() , stability
implies causality. Consequently, the impulse response of the filter
, stability
implies causality. Consequently, the impulse response of the filter
![]() is zero for
is zero for ![]() . If
. If ![]() were noncausal, all impulse-response components
were noncausal, all impulse-response components
![]() for
for ![]() would be approximated by zero.
would be approximated by zero.