The analysis portion of PARSHL returns a set of amplitudes
![]() , frequencies
, frequencies
![]() , and phases
, and phases
![]() ,
for each frame index
,
for each frame index ![]() , with a ``triad'' (
, with a ``triad'' (
![]() ) for each track
) for each track ![]() . From this analysis data the
program has the option of generating a synthetic sound.
. From this analysis data the
program has the option of generating a synthetic sound.
The synthesis is done one frame at a time. The frame at hop ![]() ,
specifies the synthesis buffer
,
specifies the synthesis buffer
![$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m \cos [n\hat{\omega}_{r}^m + \hat{\theta}_{r}^m]$](img3074.png) |
(H.9) |
The parameter interpolation across time used in PARSHL is the same
as that used by McAulay and Quatieri [174]. Let
(
![]() ) and
(
) and
(
![]() ) denote the sets of
parameters at frames
) denote the sets of
parameters at frames ![]() and
and ![]() for the
for the ![]() th frequency track.
They are taken to represent the state of the signal at time 0
(the
left endpoint) of the frame.
th frequency track.
They are taken to represent the state of the signal at time 0
(the
left endpoint) of the frame.
The instantaneous amplitude
![]() is easily obtained by linear
interpolation,
is easily obtained by linear
interpolation,
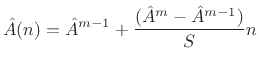 |
(H.10) |
Frequency and phase values are tied together (frequency is the phase
derivative), and they both control the instantaneous phase
![]() . Given that four variables are affecting the
instantaneous phase:
. Given that four variables are affecting the
instantaneous phase:
![]() , and
, and
![]() , we need at least
three degrees of freedom for its control, while linear interpolation
only gives one. Therefore, we need at least a cubic polynomial as
interpolation function, of the form
, we need at least
three degrees of freedom for its control, while linear interpolation
only gives one. Therefore, we need at least a cubic polynomial as
interpolation function, of the form
| (H.11) |
| (H.12) |
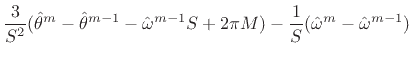 |
(H.13) | ||
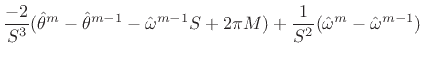 |
(H.14) |
![$\displaystyle x= {1\over 2\pi} \left[(\hat{\theta}^{m-1} + \hat{\omega}^{m-1} S - \hat{\theta}^m) + (\hat{\omega}^m - \hat{\omega}^{m-1}) {S\over 2}\right]$](img3089.png) |
(H.15) |
![$\displaystyle s^m(n) = \sum_{r=1}^{R^m} \hat{A}_{r}^m(n) \cos [\hat{\theta}_{r}^m(n)]$](img3090.png) |
(H.16) |
Figure H.5 shows the result of the analysis/synthesis process using phase information and applied to a piano tone.
![\includegraphics[width=\twidth]{eps/fig8}](img3091.png) |