Wind Instruments

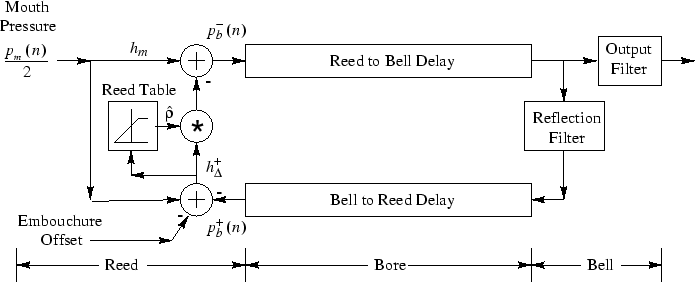
A basic DW model for a single-reed woodwind instrument, such as a clarinet, is shown in Fig. 8 [63,54,71].

Waveguide model of a single-reed, cylindrical-bore woodwind, such as a clarinet. [From [71]]fig:fSingleReedWGM

When the bore is cylindrical (plane waves) or conical (spherical waves), it can be modeled quite simply using a bidirectional delay line [54]. Because the main control variable for the instrument is air pressure in the mouth at the reed, it is convenient to choose pressure wave variables. Thus, the delay-lines carry left-going and right-going pressure samples $p_b^{+}$ and $p_b^{-}$ (respectively) which represent the traveling pressure-wave components within the bore.

To first order, the bell passes high frequencies and reflects low frequencies, where ``high'' and ``low'' frequencies are divided by the wavelength which equals the bell's diameter. Thus, the bell can be regarded as a simple ``cross-over'' network, as is used to split signal energy between a woofer and tweeter in a loudspeaker cabinet. For a clarinet bore, the nominal ``cross-over frequency'' is around $1500$ Hz [4].

The reflection filter at the right of the figure implements the bell or tone-hole losses as well as the round-trip attenuation losses from traveling back and forth in the bore. The bell output filter is highpass, and power complementary with respect to the bell reflection filter. Power complementarity follows from the assumption that the bell itself does not vibrate or otherwise absorb sound. The bell is also amplitude complementary [71].

The reed is modeled as a signal- and embouchure-dependent nonlinear reflection coefficient terminating the bore. Such a model is possible because the reed mass is neglected. The player's embouchure controls damping of the reed, reed aperture width, and other parameters, and these can be implemented as parameters on the contents of the lookup table or nonlinear function.

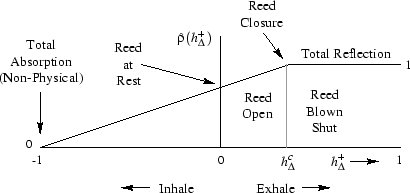
Equation (11) below shows a simple function that can be sampled and loaded into a reed table. The controlling mouth pressure is denoted $p_m$. The reflection-coefficient of the reed is denoted $\rho(h_{\Delta}^{+})$, where $h_{\Delta}^{+}\isdeftext p_b^{-}/2 - p_b^{+}$ (``incoming half-pressure-drop''). A simple choice of embouchure control is a simple additive offset in the reed-table address. Since the main feature of the reed table is the pressure-drop where the reed begins to open, such a simple offset can implement the effect of biting harder or softer on the reed, or changing the reed stiffness.

Simple, qualitatively chosen reed table for the digital waveguide clarinet. [From [71]]fig:fReedTable

In the field of computer music, it is customary to use simple piecewise linear functions for functions other than signals at the audio sampling rate, e.g., for amplitude envelopes, FM-index functions, and so on [49,48]. Along these lines, good initial results were obtained [63] using the simplified qualitatively chosen table

$$\hat\rho (h_{\Delta}^{+}) = \left\{ \begin{array}{ll} 1-m(... ...h_{\Delta}^c\leq h_{\Delta}^{+}\leq 1 \\ \end{array} \right.$$ (11)

depicted in Fig. 9 for $m=1/(h_{\Delta}^c+1)$. The corner point $h_{\Delta}^c$ is the smallest pressure difference giving reed closure. Embouchure and reed stiffness correspond to the choice of offset $h_{\Delta}^c$ and slope $m$. Brighter tones are obtained by increasing the curvature of the function as the reed begins to open; for example, one can use $\hat\rho ^k(h_{\Delta}^{+})$ for increasing $k\geq1$.

Another variation is to replace the table-lookup contents by a piecewise polynomial approximation. While less general, good results have been obtained in practice [13,14,15].

An intermediate approach between table lookups and polynomial approximations is to use interpolated table lookups. Typically, linear interpolation is used, but higher order polynomial interpolation can also be considered [71].

STK software [11] implementing a model as in Fig. 8 can be found in the file Clarinet.cpp.