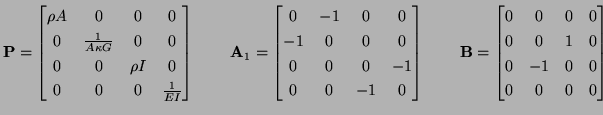Next: Dispersion
Up: Applications in Vibrational Mechanics
Previous: Free End
Timoshenko's Beam Equations
Timoshenko's theory of beams constitutes an improvement over the Euler-Bernoulli theory, in that it incorporates shear and rotational inertia effects [77]. This is one of the few cases in which a more refined modeling approach allows more tractable numerical simulation; the reason for this is that Timoshenko's theory gives rise to a hyperbolic system, unlike the Euler-Bernoulli system, for which propagation velocity is unbounded. It is this partially parabolic character of the Euler-Bernoulli system which engenders severe restrictions on the maximum allowable time step (at least in the case of explicit methods, of which type are all the scattering-based methods included in this work). For a physical derivation of Timoshenko's system, we refer the reader to [77,146,152,187,188], and simply present it here:
 |
(5.17a) |
As before, 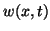 represents the transverse displacement of the beam from an equilibrium state, and the new dependent variable
represents the transverse displacement of the beam from an equilibrium state, and the new dependent variable 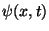 is the angle of deflection of the cross-section of the beam with respect to the vertical direction. Here, the quantities
is the angle of deflection of the cross-section of the beam with respect to the vertical direction. Here, the quantities 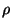 ,
, 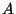 ,
, 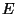 and
and  are as for the Euler-Bernoulli Equation (5.1).
are as for the Euler-Bernoulli Equation (5.1).  is the shear modulus (usually called
is the shear modulus (usually called 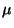 in other contexts) and
in other contexts) and 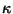 is a constant which depends on the geometry of the beam. For generality, we assume that all these material parameters are functions of
is a constant which depends on the geometry of the beam. For generality, we assume that all these material parameters are functions of  . Losses or sources are not modeled.
. Losses or sources are not modeled.
Nitsche [131], in his MDWD network-based approach preferred to use the more fundamental set of four first order PDEs from which system (5.16) is condensed:
 |
(5.18a) |
|
 |
(5.19a) |
|
We have introduced here the quantities
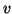 is interpreted as transverse velocity,
is interpreted as transverse velocity, 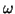 as an angular velocity,
as an angular velocity, 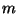 as the bending moment, and
as the bending moment, and 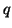 as the shear force on the cross-section. Each of the subsystems (5.17) and (5.18) has the form of a lossless (1+1)D transmission line system; they are coupled by constant-proportional terms, and it is this coupling that gives the Timoshenko system its dispersive character. The Euler-Bernoulli system (5.4) is recovered in the limit as
as the shear force on the cross-section. Each of the subsystems (5.17) and (5.18) has the form of a lossless (1+1)D transmission line system; they are coupled by constant-proportional terms, and it is this coupling that gives the Timoshenko system its dispersive character. The Euler-Bernoulli system (5.4) is recovered in the limit as
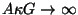 and
and
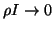 [131].
[131].
This is a symmetric hyperbolic system of the form given in (3.1), with
![$ {\bf w} = [v, q, \omega, m]^{T}$](img2370.png) ,
,
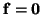 and
and
Subsections



Next: Dispersion
Up: Applications in Vibrational Mechanics
Previous: Free End
Stefan Bilbao
2002-01-22
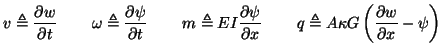
![]() ,
,
![]() and
and