Arch Carrellage is a computer music composition for organ sounds and modeled sound space. Atonal and micro tonal sources are diffused using an Ambisonics six speaker arrangement in a hexagon pattern. This composition is a triptych with subsections in each part. Aside from differences in size (length in time and duration), tempo and timbre, each section is structured as a sequence of tiles resulting from combinations of symmetric sets in the form of dyads, trichords and tetrachords, as well as threading of horizontal textures. Symmetric sets are obtained by combining two different (perhaps orthogonal) tone rows (more about this below). Besides geometrical patterns, this piece is a search for clusters of diffused sound sources, such as those heard on Philadelphia's Saints Peter and Paul Cathedral. Reverberation on an enclosed space such as this, is also a symmetrical feature, in spite of differences in perspectives, formant sections, and intersections of thousands of reflections that come from sound sources and walls in the cathedral. We can pinpoint that these reflections are like those images induced when a hexagon is divided in twelve equal parts, to get another circumscribed hexagon and further joining all points and edges thereby creating equilateral triangles inside each hexagon, in addition to a bunch of other circumscribed geometric forms (provided perception is exercised). But on its conception, this piece focuses on symmetrical structures related to pitches that construct each element on each part.

Sound wise, this piece experiments on sonority and textures resulting from blends on a myriad of timbres that hold the Organ adjective. It also touches upon atonal and micro tonal combinations of musical events in contrast to traditional tempered organ sounds. Sources come from own recordings, samples and modeled acoustics of the organ. Signal processing on some of these sources enhance gestures which cannot be achieved by any other means. Sequences of notes product of algorithmic output and computer aided composition triggered every part on this composition. For this purpose, a set of tools was developed in Lisp and Scheme by the composer, for assisting in processing of tone-rows that give symmetrical combinations, in addition to Rick Taube's Common Music (CM). Bill Shottstaedt's S7, Snd, and Common Lisp Music (CLM), as well as Joe Anderson's Ambisonics Toolkit (ATK) and Fernando Lopez-Lezcano's Dlocsig, still are extremely useful programs for synthesis and signal processing.

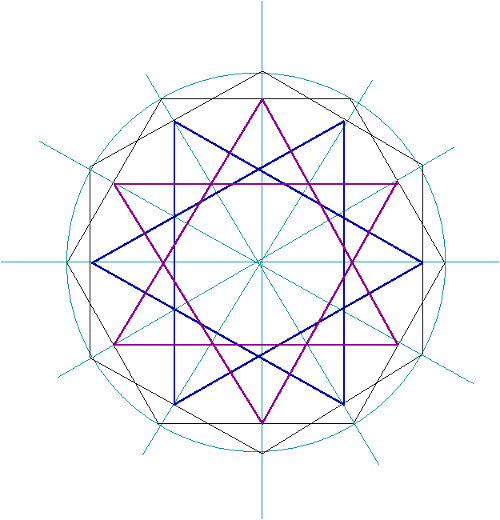
Figure No.1: Basic tile (or template) from the Herat Pattern.

In this figure two hexagons can be perceived inside a circle. They result from dividing the circle with diameters to get twelve equal parts. Further in, there are four circumscribed triangles that in turn form rhomboids and other polygons traced inside the outer hexagons. Since outer hexagons are symmetric, it is expected that inner divisions give more symmetries. Same with the four equilateral triangles that share a common center. Note that shapes on these divisions provide further symmetry. Consequently and by their symmetric properties these figures are also, rotations, tilts, mirror and transpositions, among others. Operations like those outline above can manipulate sequences of notes in the form of symmetric dyads, trichords and tetrachords that come form a tone-row.

Working with symmetries:

For the structure of Arch Carrellage, the goal was to follow a symmetric figure known as the Herat Pattern, named after the Herat Mosque in Afghanistan. At first sight patterns of hexagons, crosses, rhomboids, diamonds and stars can be perceived and recognized. Further into the Herat pattern, irregular pentagons as well as rhomboids standout. Interesting enough, six smaller triangles inside a hexagon also come into perception (see figure No,1). These triangles are also centered on a smaller hexagon and consequently, six little hexagons with equilateral triangles at their center cast this figure. Thus, from a visual perspective the Herat pattern demonstrates perception at various levels.

Worth to point out, hexagons are an outstanding example of symmetry. By joining, or flapping, several hexagons, we get honeycomb patterns, known as one of the most basic of tilings, but also a template for more symmetric patterns. To get a Herat pattern we need two hexagons plus four inscribed equilateral triangles. Outer hexagon is divided into twelve equal parts. The second inner hexagon is drawn by joining the middle points of the outer hexagon. The bases of the first inner triangles are drawn by joining points of opposite sides of the inner hexagon. These lines are parallel sides of each triangle and go from the endpoints of these parallels to the opposite equilateral triangles which overlap each other (see figure again). The parallel bases for the second equilateral triangles are drawn from midpoints of adjacent sides of the inner hexagon. Recall we had divided the outer hexagon into twelve equal parts. The sides of the second triangle are drawn from the bases to the midpoints of the upper and lower adjacent sides of the inner hexagons. Twelve divisions of the outer hexagon help find these midpoints.

Composition with the above:

Arch Carrellage is seeded on two tonerows are borrowed from Luigi Dallapiccola, lyric compositions Preguiere and Parole di San Paolo. Two rows because they resemble a cross, although not necessarily horizontal or vertical but almost orthogonal so that they have one point (note) in common. Nevertheless intersecting points slide from top to bottom, or from right to left. This, in order to achieve symmetries on their tetrachordal or trichordal combinations. While working with tone rows, basic symmetries are obtained by mirroring the row, by inverting its intervals, or by cycling the position of each note in the row. With these operations we get cycles, rotations and palindromic musical shapes. For compositional purposes these figures work as they do on geometrical analogies such as symmetric figures as in basic honeycombs.

From a musical perspective, mapping of the above geometry, takes into account that size translates into length and duration, but regardless of patterns, translations, rotations, shrinking or enlarging as repetition processes, we need to isolate or constraint parameters so that we can map visual shapes into music events. Since analogies of these shapes can establish counterparts in the sound domain, the process of generating geometric patterns and compositions with these figures on the plane or space, gives a parallel for generating musical ideas. Visual mapping of these figures don't have exact correspondence on the musical domain and vice versa. However, operations to generate other symmetries and more shapes are analogous in both domains. (i.e by rotating a square, we get a diamond. In a diamond there are two equilateral triangles tat can also be tilted. Similarly a tetrachord can be rotated so that we have a palindrome of its pitches. Dyads in this tetrachord can also be tilted so that we get other variants of the original symmetry -see Figure No.2-.)

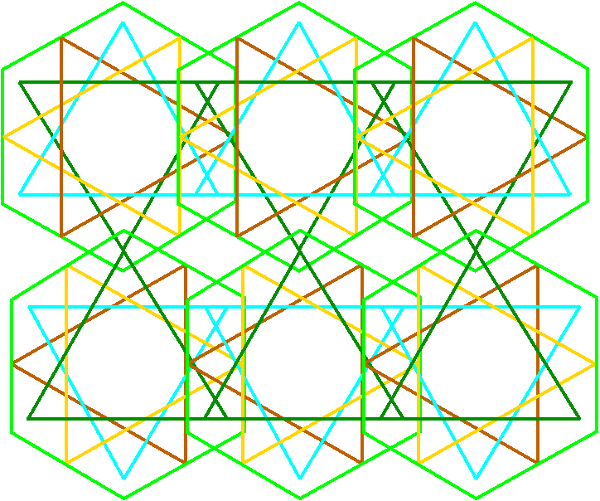
Figure No.2: Tesselations and tilings using the Herat Pattern.

In a further dimension, rotations, translations, transpositions and folding of the basic Herat Pattern create more symmetrical shapes which now can tease the mind. By the same token in the musical domain, these operations generate variations on a tone row, thereby creating symmetries on left and right hexachords, left, center, right terachords, and the four triads. Mind constructions of this type produce generative grammars that help on the cognitive features of perception while trying to make sense of shape an structure on either visual domain or sound domain.

Intuitively a hexagon can be used as a template to get combinations of notes for tetrachords, a triangle for triads, and so on. But knowing that a hexagon casts such a symmetric structure, why not go further?. By transposition or rotations, a symmetric shape creates more symmetries. With this axiom we can assume that two symmetrical combinations of tetrachords can generate more structural shapes, closely related to the original by means of symmetry (i.e. Two opposed triangles can be perceived as a diamond. Two opposed triads can generate a symmetric tetrachord, though an axis note needs to be found so that the triads unfold similarly top or bottom, left and right.)

Prime forms of each row are labeled as T₀ and P₀, respectively. Subscripts give the number of transposition of the prime form. Palindromic and inverted versions of these primes are labeled RIT₀ et RIP₀, respectively. By arithmetic operations (or rather permutations) and by listening, we found that combinations T₀, P₀; T₁, P₁; T₆, P₆; in addition to, RIT₁₀, RIP₁₀; RIT₁₁, RIP₁₁; RIT₆, RIP₆; are primes and variations, suitable for creating symmetries. By assigning six of these variations to the edges of the hexagon, we create paths to each of the other five edges to find combinations of rows an variations. Hexachords for horizontal sequences are the result of combinations of these edges; hexachords can also be used to get dyads and triads vertically. If these hexagons are used, we can also build a square symmetric matrix with combinations of the patterns found in each hexagon. In this fashion we end up with a six-by-six matrix with no horizontal or vertical contiguous same kind hexachords.

( Arch Carrellage, una composición para sonidos de Órgano, tratamiento de señal y espacio acústico modelado en computadora)

[ ¡ Actualizando traducción al castellano!. ]