Dos retos importantes surgieron en la realización de Esquemas de Marimonda. En
primera instancia, el dispositivo de amplificación, sus altavoces y
conexiones. En segunda instancia, la composición y generación de cada
sonido. Para la amplificación se utilizó un circuito genérico de
![]() con la posibilidad de corriente alterna, además de un
dispositivo para cambios en la ganancia (volumen); la entrada de este
amplificador está conectada directamente a un reproductor del tipo
tocadiscos de disco compacto portátil. Las salidas del amplificador
se conectan a dos transductores que producen la imagen
estereofónica. Los transductores están colocados en dos cajas de
resonancia con guías de onda para que el sonido no sea directo. La
respuesta de frecuencia en estos dispositivos de altavoz oscila entre
los
con la posibilidad de corriente alterna, además de un
dispositivo para cambios en la ganancia (volumen); la entrada de este
amplificador está conectada directamente a un reproductor del tipo
tocadiscos de disco compacto portátil. Las salidas del amplificador
se conectan a dos transductores que producen la imagen
estereofónica. Los transductores están colocados en dos cajas de
resonancia con guías de onda para que el sonido no sea directo. La
respuesta de frecuencia en estos dispositivos de altavoz oscila entre
los ![]() y los
y los ![]()
El desarrollo de cada timbre fue realizado utilizando síntesis de audio por frecuencia modulada (FM) especificada en la Síntesis de espectros de audio complejos por medio de modulación de frecuencias13 y, en la Introducción a la FM14. Para el movimiento espacial en cada sonido, se utilizaron técnicas propias desarrolladas con el objeto de lograr panorámicos basados en cambios de la intensidad en cada uno de los canales esterofónicos. Estas técnicas se basan en movimiento y trayectorias de vectores con funciones sinusoidales de espirógrafo y figuras de Lissajous15. Las ecuaciones para generar los factores de ganancia utilizando la técnica del espirógrafo en cada uno de los canales son:
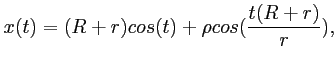
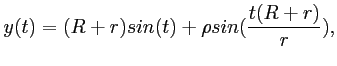
donde, ![]() es el radio mayor,
es el radio mayor, ![]() el radio menor,
el radio menor, ![]() la distancia
del centro al punto donde se genera la función circular. Si
la distancia
del centro al punto donde se genera la función circular. Si ![]() son
valores que cambian al transcurrir el tiempo y que van al menos en un
periódo de las funciones seno o coseno, es decir entre
son
valores que cambian al transcurrir el tiempo y que van al menos en un
periódo de las funciones seno o coseno, es decir entre ![]() y
y
![]()
![]() es el factor que se utiliza para atenuar la ganancia
del canal de audio
es el factor que se utiliza para atenuar la ganancia
del canal de audio ![]() y
y ![]() es el factor que se utiliza para
atenuar la ganancia del canal de audio
es el factor que se utiliza para
atenuar la ganancia del canal de audio ![]() en un sonido
estereofónico. En el caso de las figuras Lissajous se pueden utilizar
las siguientes ecuaciones paramétricas:
en un sonido
estereofónico. En el caso de las figuras Lissajous se pueden utilizar
las siguientes ecuaciones paramétricas:
donde ![]() y
y ![]() son factores para el tamaño de la figura,
son factores para el tamaño de la figura, ![]() y
y
![]() son parámetros para el numero de ciclos y
son parámetros para el numero de ciclos y ![]() valores que
cambian al transcurrir el tiempo entre entre
valores que
cambian al transcurrir el tiempo entre entre ![]() y
y ![]() En
este caso también
En
este caso también ![]() es el factor que se utiliza para atenuar la
ganancia del canal de audio 1 y
es el factor que se utiliza para atenuar la
ganancia del canal de audio 1 y ![]() es el factor que se utiliza
para atenuar la ganancia del canal de audio 2 en un sonido
estereofónico.
es el factor que se utiliza
para atenuar la ganancia del canal de audio 2 en un sonido
estereofónico.
Para la manipulación del ritmo y de la intensidad, se utilizaron algoritmos que ayudan a componer accelerandi o ritardandi y, crescendi o decrescendi. La combinación de ambos parámetros (intensidad y duración), crea efectos interesantes en la percepción conocidos como las paradojas del ritmo16 o tonos de Shepard 17. Por lo tanto en referencia a la duración, hay sonidos continuos y con el adjetivo de masa sonora, pero también hay sonidos secos y dinámicos con accelerandi y crescendi o viceversa.
|
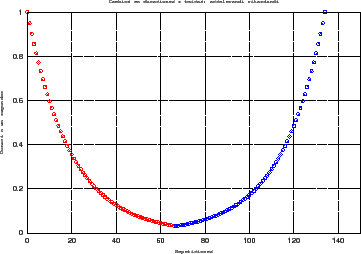
La formula para cambios en una duración cada vez mas corta (accelarandi) o cada vez mas larga (ritardandi), están basados en funciones de Gauss o gaussianas. Estas funciones comenzaron a ser utilizadas en las artes a comienzos de los años setenta por Keneth Knowlton (lado de cine y animación) y Jean Claude Risset (lado de música y acústica), como parte de experimentos realizados en los laboratorios de la Bell Telephone en Nueva Jersey en la época18. La función utilizada para manipulación de duraciones es:
donde:
![]() con
con ![]() como el máximo de
repeticiones y
como el máximo de
repeticiones y
![]() La gráfica de valores para
La gráfica de valores para
![]() repeticiones puede verse en la figura 3. Para cambios
en la intensidad de un sonido que se repite
repeticiones puede verse en la figura 3. Para cambios
en la intensidad de un sonido que se repite ![]() veces, creando un
efecto decresendo o decrescendo, se puede utilizar una
función gaussiana 19, como:
veces, creando un
efecto decresendo o decrescendo, se puede utilizar una
función gaussiana 19, como:
donde:
![]() con
con ![]() como el máximo de
reiteraciones,
como el máximo de
reiteraciones, ![]() y
y ![]() como el parámetro de
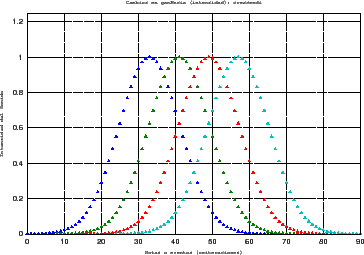
convexidad. Con
como el parámetro de
convexidad. Con
![]() y,
y, ![]() se produce la curva de
amplitud (factor de ganancia) de la figura 4.
se produce la curva de
amplitud (factor de ganancia) de la figura 4.
|
Al igual que los algoritmos para generar sonidos con síntesis de audio
FM, estas funciones fueron transcritas al lenguaje de programación
SCHEME, para producir archivos sonoros en el programa
SND20. El algoritmo para la generación de un sonido
básico con síntesis FM, está descrito en Introducción a la
Plástica Sonora21. El algoritmo en código de
Matlab para la manipulación espacial del sonido función del
tiempo, se puede ver en el apéndice![]() , listado 1. El
código correspondiente en SCHEME, se aprecia en el listado
2
, listado 1. El
código correspondiente en SCHEME, se aprecia en el listado
2![]() .
.
![]()
© Copyright 2001-2008 CCRMA, Stanford University. All rights reserved.
Created and Mantained by Juan Reyes