SOUND RADIATION

Sound is radiated from a fully or partially open tonehole because the air just outside the tonehole is disturbed by the vibrational motion of the ``open'' part of the tonehole volume. Hence the flow $U_e$ exiting the hole equals the flow through the inertance:

$$U_{e} = \frac{P_3}{j \omega L}$$ (14)

A woodwind tonehole may be considered as an isotropic source [4]. Given a source-strength 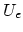$U_{e}$, the radiation pressure at a distance 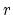$r$ from such a source is:

$$P_{rad}(r) = \left(\frac{j \omega \rho}{4 \pi r}\right) U_{e} \, e^{-j k r},$$ (15)

where $k=\omega/c$ is the free space wave velocity. By combining (14) and (15), we can compute the pressure radiated from a woodwind tonehole as:

$$P_{rad}(r) = \left(\frac{\rho}{4 \pi r L}\right) P_3 \, e^{-j k r}$$ (16)

Note that the frequency term 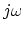$j \omega$ has disappeared in the final result. The term 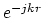$e^{-jkr}$ represents a pure time-delay (i.e., the time it takes for a radiated pressure wave to reach the ``listening point''). Thus, the radiated pressure at any distance from the tonehole can be computed by simply scaling and delaying the bore pressure $P_3$ just underneath the tonehole. We can incorporate this into the wave digital tonehole model by formulating the digital domain version of (16) as:

$$P_{rad}(r) = \left(\frac{g}{r}\right) \, \xi \, P_{3} \, z^{-N},$$ (17)

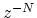where $z^{-N}$ represents a delay-line of fractional length $N = r/(cT)$, and where $\xi = S_{b}/(4 \pi t_e)$ is a constant. It must be noted that eq. (17) gives a good approximation at lower frequencies, but the accuracy decreases for higher frequencies. This is mainly because the WD tonehole model is based on a low-frequency approximation of the real acoustical behaviour of the tonehole. Moreover, we have assumed that the radiation is isotropic (i.e., the flow spreads out evenly in all directions). This assumption is valid for low frequencies, but for higher frequencies the effects of directivity need to be taken into account (such as described in [11]). Since the higher frequencies are relevant from a perceptual point of view, an extra filter (that compensates for the deviations described above) can be applied to the pressure calculated with eq. (17) in order to obtain a better aural result. In general, such a filter has a rather ``smooth'' high-pass amplitude response, and can be approximated with a lower-order digital filter.