Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Thiran Allpass Interpolators
Given a desired delay
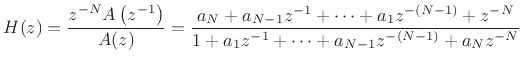 samples, an order
samples, an order  allpass filter
allpass filter
can be designed having maximally flat group delay equal to
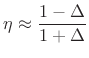 at dc using the formula
at dc using the formula
where
denotes the 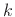 th binomial coefficient [497]. Note, incidentally,
that a lowpass filter having maximally flat group-delay at dc is
called a Bessel filter [365, pp. 228-230].
th binomial coefficient [497]. Note, incidentally,
that a lowpass filter having maximally flat group-delay at dc is
called a Bessel filter [365, pp. 228-230].
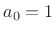 without further scaling
without further scaling
- For sufficiently large
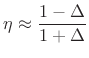 , stability is guaranteed
, stability is guaranteed
Rule of thumb:
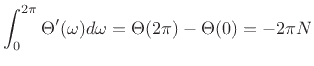
- It can be shown that the mean group delay of any stable
 th-order allpass filter is
th-order allpass filter is  samples
[452].5.8
samples
[452].5.8
- Only known closed-form case for allpass interpolators of arbitrary order
- Effective for delay-line interpolation needed for tuning since
pitch perception is most acute at low frequencies.
- Since Thiran allpass filters have maximally flat group-delay at
dc, like Lagrange FIR interpolation filters, they can be considered
the recursive extension of Lagrange interpolation.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() samples, an order
samples, an order ![]() allpass filter
allpass filter
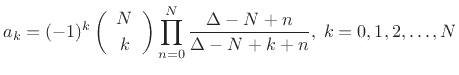
![$\displaystyle a_k=(-1)^k\left(\begin{array}{c} N \\ [2pt] k \end{array}\right)\prod_{n=0}^N\frac{\Delta-N+n}{\Delta-N+k+n},
\; k=0,1,2,\ldots,N
$](img1123.png)
![$\displaystyle \left(\begin{array}{c} N \\ [2pt] k \end{array}\right) = \frac{N!}{k!(N-k)!}
$](img1124.png)