Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Referring again to Fig.B.4, we can write the
tangential velocity vector
 as a vector cross product of
the angular-velocity vector
as a vector cross product of
the angular-velocity vector
 (§B.4.11) and the position
vector
(§B.4.11) and the position
vector
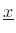 :
:
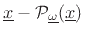 |
(B.17) |
To see this, let's first check its direction and then its magnitude.
By the right-hand rule,
 points up out of the page in
Fig.B.4. Crossing that with
points up out of the page in
Fig.B.4. Crossing that with
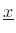 , again by the right-hand
rule, produces a tangential velocity vector
, again by the right-hand
rule, produces a tangential velocity vector
 pointing as shown
in the figure. So, the direction is correct. Now, the magnitude:
Since
pointing as shown
in the figure. So, the direction is correct. Now, the magnitude:
Since
 and
and
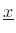 are mutually orthogonal, the angle between them
is
are mutually orthogonal, the angle between them
is 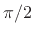 , so that, by Eq.(B.16),
, so that, by Eq.(B.16),
as desired.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() as a vector cross product of
the angular-velocity vector
as a vector cross product of
the angular-velocity vector
![]() (§B.4.11) and the position
vector
(§B.4.11) and the position
vector
![]() :
: