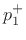 |
Consider a plane wave with peak pressure amplitude ![]() propagating
from wave impedance
propagating
from wave impedance ![]() into a new wave impedance
into a new wave impedance ![]() , as shown in
Fig.C.15. (Assume
, as shown in
Fig.C.15. (Assume ![]() and
and ![]() are real and positive.)
The physical constraints on the wave are that
are real and positive.)
The physical constraints on the wave are that
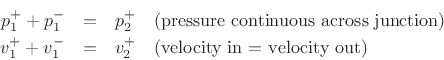
As derived in §C.7.3, we also have the Ohm's law relations:
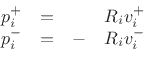
These equations determine what happens at the junction.
To obey the physical constraints at the impedance discontinuity, the
incident plane-wave must split into a reflected plane wave
![]() and a transmitted plane-wave
and a transmitted plane-wave ![]() such that
pressure is continuous and signal power is conserved. The physical
pressure on the left of the junction is
such that
pressure is continuous and signal power is conserved. The physical
pressure on the left of the junction is
![]() , and the
physical pressure on the right of the junction is
, and the
physical pressure on the right of the junction is
![]() , since
, since ![]() according to our set-up.
according to our set-up.