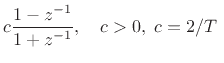 (typically) (typically) |
(8.6) | ||
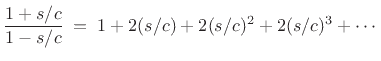 |
(8.7) |
The bilinear transform is defined by the substitution
It can be seen that analog dc (![]() ) maps to digital dc (
) maps to digital dc (![]() ) and
the highest analog frequency (
) and
the highest analog frequency (![]() ) maps to the highest digital
frequency (
) maps to the highest digital
frequency (![]() ). It is easy to show that the entire
). It is easy to show that the entire ![]() axis
in the
axis
in the ![]() plane (where
plane (where
![]() ) is mapped exactly
once around the unit circle in the
) is mapped exactly
once around the unit circle in the ![]() plane (rather than
summing around it infinitely many times, or ``aliasing'' as it does in
ordinary sampling). With
plane (rather than
summing around it infinitely many times, or ``aliasing'' as it does in
ordinary sampling). With ![]() real and positive, the left-half
real and positive, the left-half ![]() plane maps to the interior of the unit circle, and the right-half
plane maps to the interior of the unit circle, and the right-half ![]() plane maps outside the unit circle. This means stability is
preserved when mapping a continuous-time transfer function to
discrete time.
plane maps outside the unit circle. This means stability is
preserved when mapping a continuous-time transfer function to
discrete time.
Another valuable property of the bilinear transform is that
order is preserved. That is, an ![]() th-order
th-order ![]() -plane transfer
function carries over to an
-plane transfer
function carries over to an ![]() th-order
th-order ![]() -plane transfer function.
(Order in both cases equals the maximum of the degrees of the
numerator and denominator polynomials [452]).8.6
-plane transfer function.
(Order in both cases equals the maximum of the degrees of the
numerator and denominator polynomials [452]).8.6
The constant ![]() provides one remaining degree of freedom which can be used
to map any particular finite frequency from the
provides one remaining degree of freedom which can be used
to map any particular finite frequency from the ![]() axis in the
axis in the ![]() plane to a particular desired location on the unit circle
plane to a particular desired location on the unit circle
![]() in the
in the ![]() plane. All other frequencies will be warped. In
particular, approaching half the sampling rate, the frequency axis
compresses more and more. Note that at most one resonant frequency can be
preserved under the bilinear transformation of a mass-spring-dashpot
system. On the other hand, filters having a single transition frequency,
such as lowpass or highpass filters, map beautifully under the bilinear
transform; one simply uses
plane. All other frequencies will be warped. In
particular, approaching half the sampling rate, the frequency axis
compresses more and more. Note that at most one resonant frequency can be
preserved under the bilinear transformation of a mass-spring-dashpot
system. On the other hand, filters having a single transition frequency,
such as lowpass or highpass filters, map beautifully under the bilinear
transform; one simply uses ![]() to map the cut-off frequency where it
belongs, and the response looks great. In particular, ``equal ripple'' is
preserved for optimal filters of the elliptic and Chebyshev types because
the values taken on by the frequency response are identical in both cases;
only the frequency axis is warped.
to map the cut-off frequency where it
belongs, and the response looks great. In particular, ``equal ripple'' is
preserved for optimal filters of the elliptic and Chebyshev types because
the values taken on by the frequency response are identical in both cases;
only the frequency axis is warped.
The frequency-warping of the bilinear transform is readily found by
looking at the frequency-axis mapping in Eq.(7.7), i.e., by setting
![]() and
and
![]() in the bilinear-transform
definition:
in the bilinear-transform
definition:
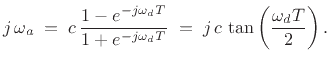
Thus, we may interpret
The bilinear transform is often used to design digital filters from analog prototype filters [346]. An on-line introduction is given in [452].