Algebraic derivation

The above equivalent forms are readily verified by deriving the transfer function from the striking-force input $f_i(n)$ to the output force signal $f_o(n)$

Referring to Fig.6.15, denote the input hammer-strike $z$ transform by $F_i(z)$ and the output signal $z$ transform by $F_o(z)$ . Also denote the loop-filter transfer function by $H_l(z)$ . By inspection of the figure, we can write

$$F_o(z) = z^{-N} \left\{ F_i(z) + z^{-2M}\left[F_i(z) + z^{-N} H_l(z)F_o(z)\right]\right\}.$$

Solving for the input-output transfer function yields

$$\begin{eqnarray*} H(z) \isdef \frac{F_o(z)}{F_i(z)} &=& z^{-N} \frac{1+z^{-2M}}{1-H_l(z)\,z^{-(2M+2N)}}\\ &=& \left(1+z^{-2M}\right)\frac{z^{-N}}{1-H_l(z)\,z^{-(2M+2N)}}\\ \end{eqnarray*}$$

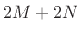
The final factored form above corresponds to the final equivalent form shown in Fig.6.17.