|
An FIR filter can be constructed in general as the difference of two IIR filters [10]. The output of the second IIR filter is delayed, scaled, and subtracted, so as to cancel the ``tail'' of the first IIR filter. The overall output is that of an FIR filter, but with great computational savings when the delay is large compared with the IIR order.
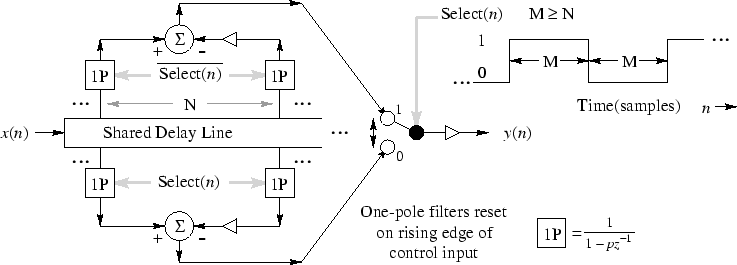
Figure 1 shows the case of a one-pole based TIIR filter which is sufficiently general for purposes of this paper; it can be configured for either a truncated growing exponential or a truncated constant impulse response. There are various choices of filter structure even in this simple case. Figure 1 shows the ``shared delay'' form. By ``pushing'' all four one-pole filters forward through the subtraction block, one obtains additionally the ``shared dynamics'' form suggested in [10]. For simplicity, however, we will describe the version in Fig. 1.
Referring to Fig. 1, suppose the upper pair of one-pole filters is
switched in (as the figure indicates). When the Select signal
transitions, the alternate one-pole pair below is selected, and the upper
one-poles can be cleared and halted (or simply not computed in a software
implementation). If the TIIR impulse-response length is ![]() samples, then
the first upper filter on the left is restarted
samples, then
the first upper filter on the left is restarted ![]() samples before it is to
be switched back in, while the second upper filter is restarted on the same sample as when it is switched back in. This works because, even
though the upper pair will not be in the same state as the lower pair after
samples before it is to
be switched back in, while the second upper filter is restarted on the same sample as when it is switched back in. This works because, even
though the upper pair will not be in the same state as the lower pair after
![]() times steps, its tail-canceling difference, which synthesizes an FIR
filter, is identical (ignoring round-off errors). Therefore, the
switching resets can be as often as every
times steps, its tail-canceling difference, which synthesizes an FIR
filter, is identical (ignoring round-off errors). Therefore, the
switching resets can be as often as every ![]() samples. It is desirable,
however, to switch much less often than every
samples. It is desirable,
however, to switch much less often than every ![]() samples in order to
minimize computations. The minimum switching rate, at the other extreme,
is determined by the exponential growth rate and available dynamic range
[10].
samples in order to
minimize computations. The minimum switching rate, at the other extreme,
is determined by the exponential growth rate and available dynamic range
[10].
Note that the multiply-add which forms the tail-canceling subtraction can be shared since only the output of the actively selected branch is needed.
Finally, we note that when the structure of Fig. 1 is used to implement a truncated constant impulse response, the one-poles become digital integrators (no multiplies), and the tail-canceling multiply-subtract becomes only a subtraction. The resets for digital integrators can be considerably less often than for growing exponentials, because the round-off error grows more slowly in an integrator [10].
In summary, a TIIR filter for making a truncated constant or rising exponential impulse response segment can be computed at a cost close to that of a one-pole filter and a multiply-add, plus some associated switching and control logic.