The Rigidly Terminated Ideal String

A rigid termination is the simplest case of a string termination. It imposes the constraint that the string cannot move at all at the termination. Let $y(t,x)$ denote the transverse displacement of an ideal vibrating string at time $t$, with $x$ denoting position along the length of the string. If we terminate a length $L$ ideal string at $x=0$ and $x=L$, we then have the ``boundary conditions''

$$\begin{eqnarray*} y(t,0) \equiv 0 \qquad y(t,L) \equiv 0 \end{eqnarray*}$$

where ``$\equiv$'' means ``identically equal to,'' i.e., equal for all $t$.

The corresponding constraints on the sampled traveling waves are then

$$\begin{eqnarray*} y^+(n) &=& -y^-(n) \\ y^-(n+N/2) &=& -y^+(n-N/2) \end{eqnarray*}$$

where $N$ is the time in samples to propagate from one end of the string to the other and back, or the total ``string loop'' delay. The loop delay is also equal to twice the number of spatial samples along the string. A digital simulation diagram for the rigidly terminated ideal string is shown in Fig. 4. A ``virtual pick-up'' is shown at the arbitrary location $x=\xi$.

Figure 4: The rigidly terminated ideal string with position output at $x=\xi$.

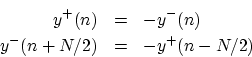
Note that rigid terminations reflect traveling displacement, velocity, or acceleration waves with a sign inversion. Slope or force waves reflect with no sign inversion. Since here we have displacement waves, the rigid terminations are inverting. This result may also be obtained from the reflection coefficient formula on the previous page by setting the terminating impedance to infinity in that formula.