Oscillator based on Complex Number Multiplication

A well known difference equation exists which can compute samples of parametrically well behaved sinusoids [1,2]. The frequency of the sinusoid can easily be changed without changing the amplitude. The equation is a property of the multiplication of two complex numbers.¹Complex numbers can be represented as two dimensional vectors in a plane in which the x axis is the real part of the number and the y axis is the imaginary part of the number. The polar coordinate form of the vector is a magnitude and an angle (measured from the x axis). The magnitude of the product of two numbers is the product of the magnitudes of the two numbers and the angle of the product is the sum of the angles of the two numbers.

We will use the following definitions and relations:

$$\begin{eqnarray*} j &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \sqrt{-1}\\ z & \... ... \\ \theta & \mathrel{\stackrel{\mathrm{\Delta}}{=}}& \angle z \end{eqnarray*}$$

In terms of real and imaginary components:

$$z=x + j y$$

where

$$\begin{eqnarray*} x &=& r\cos(\theta) \\ y &=& r\sin(\theta) \end{eqnarray*}$$

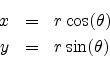
Let a sequence of complex numbers

$$z(n),\quad n=0,1,2,3,...$$

be formed from the product of two complex numbers

$$z(n+1)=z_1z(n), \protect$$ (1)

where $z_1 \mathrel{\stackrel{\mathrm{\Delta}}{=}}e^{j\theta_1} = \cos(\theta_1) + j\sin(\theta_1)$. The initial state is taken to be $z(0) = 1$, i.e., the initial magnitude and angle are $r(0)=1$ and $\theta(0)=0$, respectively. By the rules of complex number multiplication, we have

$$r(1)=r(2)= \cdots =r(n)=1$$

and

$$\theta(n) = n \theta_1.$$

The imaginary part of $z(n)$ is the desired sine wave:

$$y(n) = \sin( n \theta_1).$$

The magnitude of the sine wave is always 1. The period of the sine wave is $2\pi/\theta_1$ samples.

By changing $\theta_1$, the period can be changed without affecting the magnitude.

The actual difference equations to compute the sine wave are obtained by writing Eq.$\,$(1) as real and imaginary parts. This yields two difference equations which can be extrapolated to compute $x(n)$ and $y(n)$:

$$x(n+1) = x_1 x(n) - y_1y(n) \protect$$ (2)

$$y(n+1) = y_1x(n) + x_1y(n) \protect$$ (3)

where $x_1=\cos(\theta_1)$ and $y_1=\sin(\theta_1)$.