Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The Short Time Fourier Transform (STFT)
 is a function
of both time (frame number
is a function
of both time (frame number 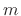 ) and frequency (
) and frequency (
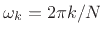 ).
It is therefore an example of a time-frequency distribution.
Others include
).
It is therefore an example of a time-frequency distribution.
Others include
The uniform and rectangular nature of the STFT time-frequency tiling
is illustrated in Fig.7.1. The window length is proportional
to the resolution cell in time, indicated by the vertical lines
in Fig.7.1. The width of the main-lobe of the
window-transform is proportional to the resolution cell in
frequency, indicated by the horizontal lines in Fig.7.1. As
detailed in Chapter 3, choosing a window length  and window
type (Hamming, Blackman, etc.) chooses the ``aspect ratio'' and total
area of the time-frequency resolution cells (rectangles
in Fig.7.1). For an example of a non-uniform time-frequency
tiling, see Fig.10.14.
and window
type (Hamming, Blackman, etc.) chooses the ``aspect ratio'' and total
area of the time-frequency resolution cells (rectangles
in Fig.7.1). For an example of a non-uniform time-frequency
tiling, see Fig.10.14.
Figure:
Example time-frequency tiling
for the STFT. Vertical line spacing indicates time resolution, and
horizontal line spacing indicates frequency resolution (both fixed
by window length and type). The area of the rectangular cells are
bounded below by the minimum time-bandwidth product (see
§B.17.1 for one definition).
![\includegraphics[width=0.8\twidth]{eps/timefreq}](img1279.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is a function
of both time (frame number
is a function
of both time (frame number ![]() ) and frequency (
) and frequency (
![]() ).
It is therefore an example of a time-frequency distribution.
Others include
).
It is therefore an example of a time-frequency distribution.
Others include
![\includegraphics[width=0.8\twidth]{eps/timefreq}](img1279.png)