Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Paraunitary systems are essentially multi-input, multi-output (MIMO)
allpass filters. Let
 denote the
denote the 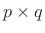 matrix transfer
function of a paraunitary system. In the square case (
matrix transfer
function of a paraunitary system. In the square case (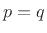 ), the
matrix determinant,
), the
matrix determinant,
![$ \det[\bold{H}(z)]$](img2195.png) , is an allpass filter.
Therefore, if a square
, is an allpass filter.
Therefore, if a square
 contains FIR elements, its determinant
is a simple delay:
contains FIR elements, its determinant
is a simple delay:
![$ \det[\bold{H}(z)]=z^{-K}$](img2196.png) for some integer
for some integer  .
.
An 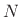 -channel analysis filter bank can be viewed as an
-channel analysis filter bank can be viewed as an 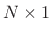 MIMO filter:
MIMO filter:
![$\displaystyle \bold{H}(z) \eqsp \left[\begin{array}{c} H_1(z) \\ [2pt] H_2(z) \\ [2pt] \vdots \\ [2pt] H_N(z)\end{array}\right]$](img2198.png) |
(12.86) |
A paraunitary filter bank must therefore satisfy
 |
(12.87) |
More generally, we allow paraunitary filter banks to scale
and/or delay the input signal:
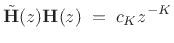 |
(12.88) |
where  is some nonnegative integer and
is some nonnegative integer and 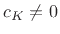 .
.
We can note the following properties of paraunitary filter banks:
- The synthesis filter bank is simply the paraconjugate of the
analysis filter bank:
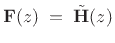 |
(12.89) |
That is, since the paraconjugate is the inverse of a paraunitary filter matrix,
it is exactly what we need for perfect reconstruction.
- The channel filters
 are power complementary:
are power complementary:
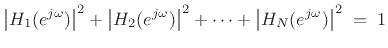 |
(12.90) |
This follows immediately from looking at the paraunitary property on the
unit circle.
- When
 is FIR, the corresponding synthesis filter matrix
is FIR, the corresponding synthesis filter matrix
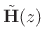 is also FIR.
is also FIR.
- When
 is FIR, each synthesis filter,
is FIR, each synthesis filter,
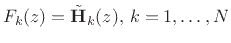 , is simply the
, is simply the
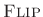 of its corresponding
analysis filter
of its corresponding
analysis filter
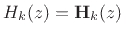 :
:
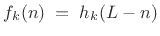 |
(12.91) |
where  is the filter length. (When the filter coefficients are
complex,
is the filter length. (When the filter coefficients are
complex,
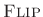 includes a complex conjugation as well.) This
follows from the fact that paraconjugating an FIR filter amounts to
simply flipping (and conjugating) its coefficients. As we observed in
(11.83) above (§11.5.2), only trivial FIR filters of
the form
includes a complex conjugation as well.) This
follows from the fact that paraconjugating an FIR filter amounts to
simply flipping (and conjugating) its coefficients. As we observed in
(11.83) above (§11.5.2), only trivial FIR filters of
the form
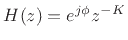 can be paraunitary in the
single-input, single-output (SISO) case. In the MIMO case, on the
other hand, paraunitary systems can be composed of FIR filters of any
order.
can be paraunitary in the
single-input, single-output (SISO) case. In the MIMO case, on the
other hand, paraunitary systems can be composed of FIR filters of any
order.
- FIR analysis and synthesis filters in paraunitary filter banks
have the same amplitude response. This follows from the fact
that
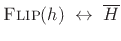 , i.e., flipping an FIR filter
impulse response
, i.e., flipping an FIR filter
impulse response 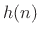 conjugates the frequency response, which does
not affect its amplitude response
conjugates the frequency response, which does
not affect its amplitude response
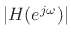 .
.
- The polyphase matrix
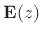 for any FIR paraunitary perfect
reconstruction filter bank can be written as the product of a
paraunitary and a unimodular matrix, where a
unimodular polynomial matrix
for any FIR paraunitary perfect
reconstruction filter bank can be written as the product of a
paraunitary and a unimodular matrix, where a
unimodular polynomial matrix
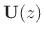 is any square
polynomial matrix having a constant nonzero
determinant. For example,
is any square
polynomial matrix having a constant nonzero
determinant. For example,
is unimodular. See
[287, p. 663] for further details.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote the
denote the ![]() matrix transfer
function of a paraunitary system. In the square case (
matrix transfer
function of a paraunitary system. In the square case (![]() ), the
matrix determinant,
), the
matrix determinant,
![]() , is an allpass filter.
Therefore, if a square
, is an allpass filter.
Therefore, if a square
![]() contains FIR elements, its determinant
is a simple delay:
contains FIR elements, its determinant
is a simple delay:
![]() for some integer
for some integer ![]() .
.
![]() -channel analysis filter bank can be viewed as an
-channel analysis filter bank can be viewed as an ![]() MIMO filter:
MIMO filter:
![$\displaystyle \bold{H}(z) \eqsp \left[\begin{array}{c} H_1(z) \\ [2pt] H_2(z) \\ [2pt] \vdots \\ [2pt] H_N(z)\end{array}\right]$](img2198.png)
![$\displaystyle \bold{U}(z) \eqsp
\left[\begin{array}{cc} 1+z^3 & z^2 \\ [2pt] z & 1 \end{array}\right] $](img2213.png)