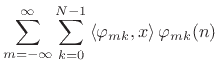Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The Short Time Fourier Transform (STFT) is defined as a time-ordered
sequence of DTFTs, and implemented in practice as a sequence of FFTs
(see §7.1). Thus, the signal basis functions are naturally
defined as the DFT-sinusoids multiplied by time-shifted windows,
suitably normalized for unit
 norm:
norm:
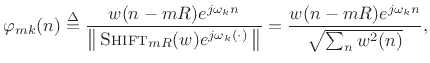 |
(12.115) |
![$\displaystyle \omega_k = \frac{2\pi k}{N}, \quad k \in [0,N-1], \quad n\in (-\infty,\infty),\quad w(n)\in{\cal R},$](img2312.png) |
(12.116) |
and  is the DFT length.
is the DFT length.
When successive windows overlap (i.e., the hop size 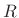 is less than
the window length
is less than
the window length  ), the basis functions are not
orgthogonal. In this case, we may say that the basis set
is overcomplete.
), the basis functions are not
orgthogonal. In this case, we may say that the basis set
is overcomplete.
The basis signals are orthonormal when  and the rectangular
window is used (
and the rectangular
window is used ( ). That is, two rectangularly windowed DFT
sinusoids are orthogonal when either the frequency bin-numbers or the
time frame-numbers differ, provided that the window length
). That is, two rectangularly windowed DFT
sinusoids are orthogonal when either the frequency bin-numbers or the
time frame-numbers differ, provided that the window length  equals
the number of DFT frequencies
equals
the number of DFT frequencies  (no zero padding). In other words,
we obtain an orthogonal basis set in the STFT when the hop size,
window length, and DFT length are all equal (in which case the
rectangular window must be used to retain the perfect-reconstruction
property). In this case, we can write
(no zero padding). In other words,
we obtain an orthogonal basis set in the STFT when the hop size,
window length, and DFT length are all equal (in which case the
rectangular window must be used to retain the perfect-reconstruction
property). In this case, we can write
![$\displaystyle \varphi_{mk}= \hbox{\sc Shift}_{mN}\left[\hbox{\sc ZeroPad}_\infty\left(\varphi_k ^{\hbox{\tiny DFT}}\right)\right],$](img2314.png) |
(12.117) |
i.e.,
![$\displaystyle \varphi_{mk}(n) = \left\{\begin{array}{ll} \frac{e^{j\omega_k n}}{\sqrt{N}}, & mN \leq n \leq (m+1)N-1 \\ [5pt] 0, & \mbox{otherwise.} \\ \end{array} \right.$](img2315.png) |
(12.118) |
The coefficient of projection can be written
so that the signal expansion can be interpreted as
In the overcomplete case, we get a special case of weighted
overlap-add (§8.6):
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() norm:
norm:
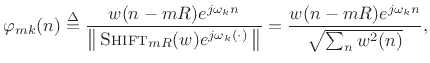
![$\displaystyle \omega_k = \frac{2\pi k}{N}, \quad k \in [0,N-1], \quad n\in (-\infty,\infty),\quad w(n)\in{\cal R},$](img2312.png)
![]() is less than
the window length
is less than
the window length ![]() ), the basis functions are not
orgthogonal. In this case, we may say that the basis set
is overcomplete.
), the basis functions are not
orgthogonal. In this case, we may say that the basis set
is overcomplete.
![]() and the rectangular
window is used (
and the rectangular
window is used (![]() ). That is, two rectangularly windowed DFT
sinusoids are orthogonal when either the frequency bin-numbers or the
time frame-numbers differ, provided that the window length
). That is, two rectangularly windowed DFT
sinusoids are orthogonal when either the frequency bin-numbers or the
time frame-numbers differ, provided that the window length ![]() equals
the number of DFT frequencies
equals
the number of DFT frequencies ![]() (no zero padding). In other words,
we obtain an orthogonal basis set in the STFT when the hop size,
window length, and DFT length are all equal (in which case the
rectangular window must be used to retain the perfect-reconstruction
property). In this case, we can write
(no zero padding). In other words,
we obtain an orthogonal basis set in the STFT when the hop size,
window length, and DFT length are all equal (in which case the
rectangular window must be used to retain the perfect-reconstruction
property). In this case, we can write
![$\displaystyle \varphi_{mk}(n) = \left\{\begin{array}{ll} \frac{e^{j\omega_k n}}{\sqrt{N}}, & mN \leq n \leq (m+1)N-1 \\ [5pt] 0, & \mbox{otherwise.} \\ \end{array} \right.$](img2315.png)

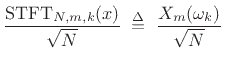
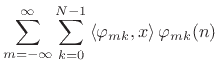
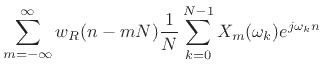
![$\displaystyle \sum_{m=-\infty}^{\infty}
\hbox{\sc Shift}_{mN,n}\left\{\hbox{\sc ZeroPad}_\infty\left[\hbox{DFT}_N^{-1}(X_m)\right]\right\}$](img2322.png)