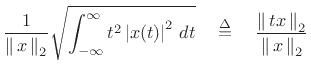 |
|||
 |
(B.61) |
More interesting definitions of duration and bandwidth are obtained
using the normalized second moments of the squared magnitude:

By the DTFT power theorem (§2.3.8), we have
![]() . Note that writing ``
. Note that writing ``
![]() '' and
``
'' and
``
![]() '' is an abuse of notation, but a convenient one.
These duration/bandwidth definitions are routinely used in physics,
e.g., in connection with the Heisenberg uncertainty principle [59].Under these definitions, we have the following theorem
[202, p. 273-274]:
'' is an abuse of notation, but a convenient one.
These duration/bandwidth definitions are routinely used in physics,
e.g., in connection with the Heisenberg uncertainty principle [59].Under these definitions, we have the following theorem
[202, p. 273-274]:
Theorem: If
![]() as
as
![]() , then
, then
| (B.63) |
Proof: Without loss of generality, we may take consider ![]() to be real
and normalized to have unit
to be real
and normalized to have unit
![]() norm (
norm (
![]() ). From the
Schwarz inequality [264],B.2
). From the
Schwarz inequality [264],B.2
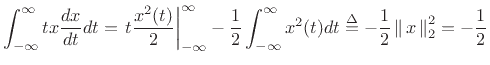 |
(B.65) |
The second term on the right-hand side of (B.65) can be evaluated using the power theorem and differentiation theorem (§B.2):
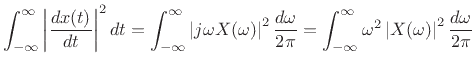 |
(B.66) |
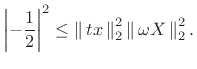 |
(B.67) |
If equality holds in the uncertainty relation (B.63), then (B.65) implies
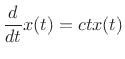 |
(B.68) |