Definition. A complex valued function of a complex variable
Any passive driving-point impedance, such as the impedance of a violin bridge, is positive real. Positive real functions have been studied extensively in the continuous-time case in the context of network synthesis [1,9]. Very little, however, seems to be available in the discrete time case. The purpose of this note (an excerpt from [7]) is to collect together some facts about positive real transfer functions for discrete-time linear systems.
Definition.
A complex valued function of a complex variable ![]() is said to be
positive real (PR) if
is said to be
positive real (PR) if
We now specialize to the subset of functions ![]() representable as a
ratio of finite-order polynomials in
representable as a
ratio of finite-order polynomials in ![]() . This class of ``rational''
functions is the set of all transfer functions of finite-order
time-invariant linear systems, and we write
. This class of ``rational''
functions is the set of all transfer functions of finite-order
time-invariant linear systems, and we write ![]() to denote a member
of this class. We use the convention that stable, minimum phase
systems are analytic and nonzero in the strict outer
disk.1 Condition (1) implies
that for
to denote a member
of this class. We use the convention that stable, minimum phase
systems are analytic and nonzero in the strict outer
disk.1 Condition (1) implies
that for ![]() to be PR, the polynomial coefficients must be real,
and therefore complex poles and zeros must exist in conjugate
pairs. We assume from this point on that
to be PR, the polynomial coefficients must be real,
and therefore complex poles and zeros must exist in conjugate
pairs. We assume from this point on that
![]() satisfies (1).
From (2) we derive the facts below.
satisfies (1).
From (2) we derive the facts below.
Theorem. A real rational function ![]() is PR iff
is PR iff
![]() .
.
Proof. Expressing ![]() in polar form gives
in polar form gives
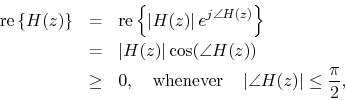
since the zeros of ![]() are isolated.
are isolated.
![]()
Proof. Assuming ![]() is PR, we have by Thm. (1),
is PR, we have by Thm. (1),
Theorem. A PR function ![]() is analytic and nonzero in
the strict outer disk.
is analytic and nonzero in
the strict outer disk.
Proof. (By contradiction)
Without loss of generality, we treat only ![]() order polynomials
order polynomials
The general (normalized) causal, finite-order, linear,
time-invariant transfer function may be written
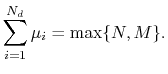
Suppose there is a pole of multiplicity ![]() outside the unit circle.
Without loss of generality, we may set
outside the unit circle.
Without loss of generality, we may set ![]() , and
, and
![]() with
with ![]() . Then for
. Then for ![]() near
near ![]() , we have
, we have

Consider the circular neighborhood of radius ![]() described by
described by
![]() . Since
. Since ![]() we may
choose
we may
choose
![]() so that all points
so that all points ![]() in this neighborhood lie
outside the unit circle. If we write the residue of the factor
in this neighborhood lie
outside the unit circle. If we write the residue of the factor
![]() in polar form as
in polar form as
![]() , then we have,
for sufficiently small
, then we have,
for sufficiently small ![]() ,
,
Corollary. In equation Eq.![]() (1),
(1), ![]() .
.
Proof. If ![]() , then there are
, then there are ![]() poles at
infinity. As
poles at
infinity. As
![]() ,
,
![]() , we must have
, we must have ![]() .
.
![]()
Corollary. The log-magnitude of a PR function has zero mean on the unit circle.
This is a general property of stable, minimum-phase transfer functions which follows immediately from the argument principle [3,4].
Corollary. A rational PR function has an equal number of poles and zeros all of which are in the unit disk.
This really a convention for numbering poles and zeros. In Eq.![]() (1),
we have
(1),
we have ![]() , and all poles and zeros inside the unit disk. Now, if
, and all poles and zeros inside the unit disk. Now, if
![]() then we have
then we have ![]() extra poles at
extra poles at ![]() induced by the numerator.
If
induced by the numerator.
If ![]() , then
, then ![]() zeros at the origin appear from the denominator.
zeros at the origin appear from the denominator.
Corollary. Every pole on the unit circle of a positive real function must be simple with a real and positive residue.
Proof. We repeat the previous argument using a semicircular neighborhood of
radius ![]() about the point
about the point
![]() to obtain
to obtain
Corollary. If ![]() is PR with a zero at
is PR with a zero at
![]() , then
, then


Proof. We may repeat the above for ![]() .
.
Theorem. Every PR function ![]() has a causal inverse z transform
has a causal inverse z transform ![]() .
.
Proof. This follows immediately from analyticity in the outer disk
[5, pp. 30-36]
However, we may give a more concrete proof as follows.
Suppose ![]() is non-causal. Then there exists
is non-causal. Then there exists
![]() such that
such that
![]() .
We have,
.
We have,

Hence, ![]() has at least one pole at infinity and cannot be PR by Thm. (1).
Note that this pole at infinity cannot be cancelled since otherwise
has at least one pole at infinity and cannot be PR by Thm. (1).
Note that this pole at infinity cannot be cancelled since otherwise

which contradicts the hypothesis that ![]() is non-causal.
is non-causal.
![]()
Theorem.
![]() is PR iff it is analytic for
is PR iff it is analytic for
![]() , poles on the
unit circle are simple with real and positive residues, and
re
, poles on the
unit circle are simple with real and positive residues, and
re![]() for
for
![]() .
.
Proof. If ![]() is positive real, the conditions stated hold by virtue
of Thm. (1) and the definition of positive real.
is positive real, the conditions stated hold by virtue
of Thm. (1) and the definition of positive real.
To prove the converse, we first show nonnegativity on the upper semicircle implies nonnegativity over the entire circle.
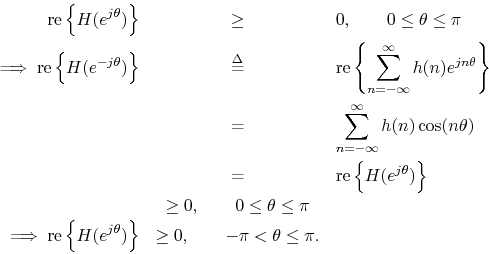
Alternatively, we might simply state that
![]() real
real
![]() re
re![]() even in
even in ![]() .
.
Next, since the function ![]() is analytic everywhere except at
is analytic everywhere except at
![]() , it follows that
, it follows that
![]() is analytic wherever
is analytic wherever
![]() is finite. There are no poles of
is finite. There are no poles of ![]() outside the unit
circle due to the analyticity assumption, and poles on the unit circle
have real and positive residues. Referring again to the limiting form
Eq.
outside the unit
circle due to the analyticity assumption, and poles on the unit circle
have real and positive residues. Referring again to the limiting form
Eq.![]() (2) of
(2) of ![]() near a pole on the unit circle at
near a pole on the unit circle at ![]() ,
we see that
,
we see that
For example, if a transfer function is known to be asymptotically stable, then a frequency response with nonnegative real part implies that the transfer function is positive real.
Note that consideration of ![]() leads to analogous necessary and sufficient
conditions for
leads to analogous necessary and sufficient
conditions for ![]() to be positive real in terms of its
zeros instead of poles.
to be positive real in terms of its
zeros instead of poles.
![]()