Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From (J.18),
we have that the reflectance seen at a continuous-time impedance
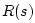 is given for force waves by
is given for force waves by
where 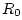 is the wave impedance connected to the impedance
is the wave impedance connected to the impedance 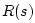 .
As discussed earlier, all passive impedances are positive real.
It can be easily verified that
.
As discussed earlier, all passive impedances are positive real.
It can be easily verified that 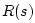 positive real implies that
positive real implies that 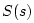 is stable and has magnitude less than or equal to
is stable and has magnitude less than or equal to  on the
on the 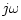 axis (and hence over the entire left-half plane, by the maximum modulus
theorem), i.e.,
axis (and hence over the entire left-half plane, by the maximum modulus
theorem), i.e.,
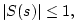
re
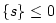
Any stable 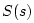 satisfying (K.1) is called a passive
reflectance.
satisfying (K.1) is called a passive
reflectance.
Solving for 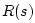 , we can characterize every passive impedance in terms
of its corresponding reflectance:
, we can characterize every passive impedance in terms
of its corresponding reflectance:
The reflectance is always defined relative to an impedance 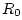 which is
the impedance attached to
which is
the impedance attached to 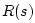 to create an impedance discontinuity and
thereby generate (frequency-dependent) reflections.
to create an impedance discontinuity and
thereby generate (frequency-dependent) reflections.
In the discrete-time case, we have the same basic relations, but in the  plane:
plane:
and
Stable functions 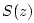 satisfying (K.1) are also known in the
mathematics literature as Schur functions. In the limit as damping
goes to zero (all poles of
satisfying (K.1) are also known in the
mathematics literature as Schur functions. In the limit as damping
goes to zero (all poles of 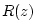 converge to the unit circle, with
interlacing zeros as required to remain positive real), the reflectance
approaches the transfer function of an allpass filter. Thus, the
Schur function is a generalization of an allpass transfer function to allow
for loss. Recalling that a lossless impedance is called a reactance,
we can say that every reactance gives rise to an allpass reflectance.
Thus, for example, waves reflecting off a mass at the end of the string
will be allpass filtered. It is intuitively very straightforward that the
reflection magnitude cannot exceed
converge to the unit circle, with
interlacing zeros as required to remain positive real), the reflectance
approaches the transfer function of an allpass filter. Thus, the
Schur function is a generalization of an allpass transfer function to allow
for loss. Recalling that a lossless impedance is called a reactance,
we can say that every reactance gives rise to an allpass reflectance.
Thus, for example, waves reflecting off a mass at the end of the string
will be allpass filtered. It is intuitively very straightforward that the
reflection magnitude cannot exceed  at any frequency when reflecting
from a passive impedance back into a passive medium at impedance
at any frequency when reflecting
from a passive impedance back into a passive medium at impedance 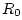 . It
is also intuitively satisfying that lossless reflection involves only a
phase shift and no amplification or attenuation at any frequency.
. It
is also intuitively satisfying that lossless reflection involves only a
phase shift and no amplification or attenuation at any frequency.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() is given for force waves by
is given for force waves by
![]() , we can characterize every passive impedance in terms
of its corresponding reflectance:
, we can characterize every passive impedance in terms
of its corresponding reflectance:
![]() plane:
plane: