Mass and Dashpot in Series

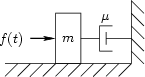
This is our first example illustrating a series connection of wave digital elements. Figure N.25 gives the physical scenario of a simple mass-dashpot system, and Fig. N.26 shows the equivalent circuit. Replacing element voltages and currents in the equivalent circuit by wave variables in an infinitesimal waveguides produces Fig. N.27.

Figure N.25: External force driving a mass which in turn drives a dashpot terminated on the other end by a rigid wall.

Figure N.26: Electrical equivalent circuit of the mass and dashpot system of Fig. N.25.

Figure N.27: Intermediate wave-variable model of the mass and dashpot of Fig. N.26.

Figure N.28: Wave digital filter for an ideal force source in parallel with the series combination of a mass $m$ and dashpot $\mu$. The parallel and series adaptors are joined at an impedance $R$ which is calculated to suppress reflection from port 1 of the series adaptor.

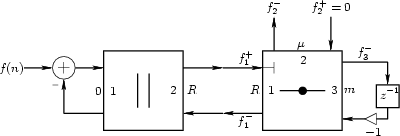The system can be described as an ideal force source $f(t)$ connected in parallel with the series connection of mass $m$ and dashpot $\mu$. Figure N.28 illustrates the resulting wave digital filter. Note that the ports are now numbered for reference. Two more symbols are introduced in this figure: (1) the horizontal line with a dot in the middle indicating a series adaptor, and (2) the indication of a reflection-free port on input 1 of the series adaptor (signal $f^{{+}}_1(n)$). Recall that a reflection-free port is always necessary when connecting two adaptors together, to avoid creating a delay-free loop.

Let's first calculate the impedance $R$ necessary to make input 1 of the series adaptor reflection free. From Eq. (N.37), we require

$$R = m + \mu$$

That is, the impedance of the reflection-free port must equal the series combination of all other port impedances meeting at the junction.

The parallel adaptor, viewed alone, is equivalent to a force source driving impedance $R=m+\mu$. It is therefore realizable as in Fig. N.19 with the wave digital spring replaced by the mass-dashpot assembly in Fig. N.28. However, we can also carry out a quick analysis to verify this: The alpha parameters are

$$\begin{eqnarray*} \alpha_1 &\isdef & \frac{2\Gamma _1}{\Gamma _1+\Gamma _2} = \... ...\mu}\right)}{\infty+\left(\frac{1}{m}+\frac{1}{\mu}\right)} = 0 \end{eqnarray*}$$

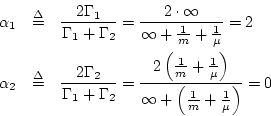
Therefore, the reflection coefficient seen at port 1 of the parallel adaptor is $\rho = \alpha_1 - 1 = 1$, and the Kelly-Lochbaum scattering junction depicted in Fig. N.19 is verified.

Let's now calculate the internals of the series adaptor in Fig. N.28. From Eq. (N.26), the beta parameters are

$$\begin{eqnarray*} \beta_1 &\isdef & \frac{2R_1}{R_1+R_2+R_3} = \frac{2(m+\mu)}{... ...R_3}{R_1+R_2+R_3} = \frac{2m}{(m+\mu)+m+\mu} = \frac{m}{m+\mu} \end{eqnarray*}$$

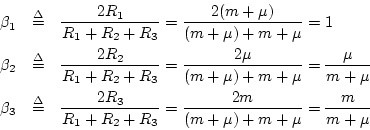
Following Eq. (N.30), the series adaptor computes

$$\begin{eqnarray*} f^{{+}}_J(n) &=& f^{{+}}_1(n)+f^{{+}}_2(n)+f^{{+}}_3(n) = f(... ...(n)\\ &=& \frac{\mu}{m+\mu}f^{{+}}_3(n) - \frac{m}{m+\mu} f(n) \end{eqnarray*}$$

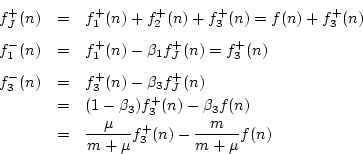
We do not need to explicitly compute $f^{{-}}_2(n)$ because it goes into a purely resistive impedance $\mu$ and produces no return wave. For the same reason, $f^{{+}}_2(n)\equiv\message{CHANGE eqv TO equiv IN SOURCE}0$. Figure N.29 shows a wave flow diagram of the computations derived, together with the result of elementary simplifications.

Figure N.29: Wave flow diagram for the WDF modeling an ideal force source in parallel with the series combination of a mass $m$ and dashpot $\mu$.

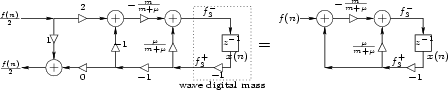Because the difference of the two coefficients in Fig. N.29 is 1, we can easily derive the one-multiply form in Fig. N.30.

Figure N.30: One-multiply form of the WDF in Fig. N.29.