Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Length 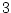 FIR Loop Filter
FIR Loop Filter
The simplest nondegenerate odd-order case is the second-order FIR case
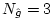 . The symmetry constraint leaves two degrees of freedom:
. The symmetry constraint leaves two degrees of freedom:
If the dc gain is normalized to unity, then
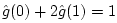 ,
and there is only one remaining degree of freedom which can be
interpreted as a damping control. As damping increased,
the duration of free vibration is reduced at all nonzero frequencies,
and the decay of higher frequencies is accelerated relative to lower
frequencies, provided
In this coefficient range, the string-loop amplitude response can be
described as a ``raised cosine'' having a unit-magnitude peak at dc,
and minimum gains
,
and there is only one remaining degree of freedom which can be
interpreted as a damping control. As damping increased,
the duration of free vibration is reduced at all nonzero frequencies,
and the decay of higher frequencies is accelerated relative to lower
frequencies, provided
In this coefficient range, the string-loop amplitude response can be
described as a ``raised cosine'' having a unit-magnitude peak at dc,
and minimum gains
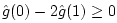 at plus and minus half the
sampling rate (
at plus and minus half the
sampling rate (
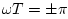 ).
).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() . The symmetry constraint leaves two degrees of freedom:
. The symmetry constraint leaves two degrees of freedom: