Energy Conservation by Newton's Second Law

Recall that Newton's second law applied to a mass-spring system, as in §E.1.5, yields

$$f_m(t) + f_k(t) = 0, \quad \forall t,$$

which leads to the differential equation obeyed by the mass-spring system:

$$m{\ddot x}(t) + k\,x(t) = 0 \quad \forall t$$

Multiplying through by 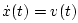${\dot x}(t)=v(t)$ gives

$$\begin{eqnarray*} 0 &=& m{\ddot x}(t){\dot x}(t) + k\,x(t){\dot x}(t)\\ &=& m\... ...c{d}{dt} \left[ E_m(t) + E_k(t) \right]\\ &=& \frac{d}{dt} E(t) \end{eqnarray*}$$

Thus, Newton's second law and Hooke's law imply conservation of energy in the mass-spring system of Fig. E.2.