Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It is desirable that the stored filter impulse response be sampled
sufficiently densely so that interpolating linearly between samples does
not introduce error greater than the quantization error. We will show that
this condition is satisfied whenever the filter table contains at least
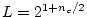 entries per zero-crossing, where
entries per zero-crossing, where 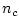 is the number of
bits allocated to each table entry.
is the number of
bits allocated to each table entry.
Linear Interpolation Error Bound.
Let 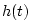 denote the lowpass filter impulse response, and assume it is
twice continuously differentiable for all
denote the lowpass filter impulse response, and assume it is
twice continuously differentiable for all  . By Taylor's theorem
[155, p. 119], we have
. By Taylor's theorem
[155, p. 119], we have
for some
![$ \lambda \in[0,1]$](img2306.png) , where
, where
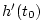 denotes the time derivative of
denotes the time derivative of
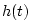 evaluated at
evaluated at 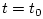 , and
, and
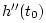 is the second derivative at
is the second derivative at
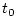 .
.
The linear interpolation error is defined as
where
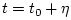 ,
,
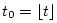 ,
,
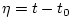 , and
, and
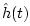 is the interpolated value given by
where
is the interpolated value given by
where
 and
and
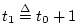 . Thus
. Thus 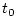 and
and 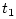 are
successive time instants for which samples of
are
successive time instants for which samples of 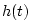 are available,
and
are available,
and
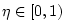 is the linear interpolation factor. (We ignore
errors in the linear interpolation itself at this point.)
is the linear interpolation factor. (We ignore
errors in the linear interpolation itself at this point.)
Expressing 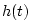 as
as
applying Eq. (I.3.4) to both terms on the right-hand side,
and subtracting Eq. (I.3.4) gives
where both 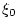 and
and 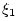 are in
are in ![$ [t_0,t_1]$](img2324.png) . Defining
and noting that
. Defining
and noting that
 for some
for some
![$ \lambda \in[0,1]$](img2306.png) which implies
we obtain the upper bound
which implies
we obtain the upper bound
Application to the Ideal Lowpass Filter.
For the ideal lowpass filter, we have
where
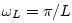 , and
, and 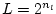 is the number of table entries per
zero-crossing.
Note that the rightmost form in Eq. (I.3.4) is simply
the inverse Fourier transform of the ideal lowpass-filter frequency
response. Twice differentiating with respect to
is the number of table entries per
zero-crossing.
Note that the rightmost form in Eq. (I.3.4) is simply
the inverse Fourier transform of the ideal lowpass-filter frequency
response. Twice differentiating with respect to 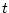 , we obtain
from which it follows that the maximum magnitude is
Note that this bound is attained at
, we obtain
from which it follows that the maximum magnitude is
Note that this bound is attained at  . Substituting Eq. (I.3.4)
into Eq. (I.3.4), we obtain the error bound
Thus for the ideal lowpass filter
. Substituting Eq. (I.3.4)
into Eq. (I.3.4), we obtain the error bound
Thus for the ideal lowpass filter
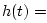 sinc
sinc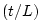 , the pointwise
error in the interpolated lookup of
, the pointwise
error in the interpolated lookup of 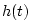 is bounded by
is bounded by 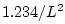 .
This means that
.
This means that 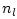 must be about half the coefficient word-length
must be about half the coefficient word-length 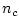 used for the filter coefficients. For example, if
used for the filter coefficients. For example, if 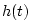 is quantized to
is quantized to
 bits,
bits, 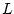 must be of the order of
must be of the order of
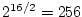 . In contrast, we
will show that without linear interpolation,
. In contrast, we
will show that without linear interpolation, 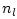 must increase
proportional to
must increase
proportional to 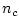 for
for 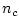 -bit samples of
-bit samples of 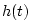 . In the
. In the  -bit
case, this gives
-bit
case, this gives
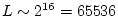 . The use of linear interpolation
of the filter coefficients reduces the memory requirements considerably.
. The use of linear interpolation
of the filter coefficients reduces the memory requirements considerably.
The error bounds obtained for the ideal lowpass filter are typically
accurate also for lowpass filters used in practice. This is because the
error bound is a function of  , the maximum curvature of the impulse
response
, the maximum curvature of the impulse
response 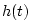 , and most lowpass designs will have a value of
, and most lowpass designs will have a value of 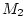 very
close to that of the ideal case. The maximum curvature is determined
primarily by the bandwidth of the filter since, generalizing equations
Eq. (I.3.4) and Eq. (I.3.4),
very
close to that of the ideal case. The maximum curvature is determined
primarily by the bandwidth of the filter since, generalizing equations
Eq. (I.3.4) and Eq. (I.3.4),
which is just the second moment of the lowpass-filter frequency response
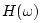 (which is real for symmetric FIR filters obtained by
symmetrically windowing the ideal sinc function [340]). A
lowpass-filter design will move the cut-off frequency slightly below that
of the ideal lowpass filter in order to provide a ``transition band'' which
allows the filter response to give sufficient rejection at the ideal
cut-off frequency which is where aliasing begins. Therefore, in a well
designed practical lowpass filter, the error bound
(which is real for symmetric FIR filters obtained by
symmetrically windowing the ideal sinc function [340]). A
lowpass-filter design will move the cut-off frequency slightly below that
of the ideal lowpass filter in order to provide a ``transition band'' which
allows the filter response to give sufficient rejection at the ideal
cut-off frequency which is where aliasing begins. Therefore, in a well
designed practical lowpass filter, the error bound 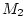 should be lower
than in the ideal case.
should be lower
than in the ideal case.
Relation of Interpolation Error to Quantization Error.
If
![$ h(t)\in[-1,1-2^{-n_c}]$](img2343.png) is approximated by
is approximated by 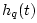 which is
represented in two's complement fixed-point
arithmetic, then
which is
represented in two's complement fixed-point
arithmetic, then
where
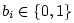 is the
is the 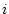 th bit,
and the worst-case rounding error is
Letting
th bit,
and the worst-case rounding error is
Letting
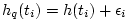 , where
, where
 ,
the interpolated look-up becomes
Thus the error in the interpolated
lookup between quantized filter coefficients is bounded by
which, in the case of
,
the interpolated look-up becomes
Thus the error in the interpolated
lookup between quantized filter coefficients is bounded by
which, in the case of
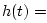 sinc
sinc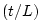 , can be written
If
, can be written
If
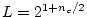 , then
, then
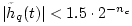 ,
and the interpolation error is less than the quantization error by more
than a factor of
,
and the interpolation error is less than the quantization error by more
than a factor of 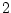 .
.
Error in the Absence of Interpolation.
For comparison purposes, we derive the error incurred when no interpolation
of the filter table is performed. In this case, assuming rounding to the
nearest table entry, we have
where
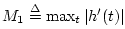 . For the ideal lowpass, we
have
. For the ideal lowpass, we
have
Note that
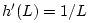 and
and
 . Thus
. Thus
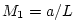 where
where
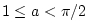 . The no-interpolation error bound is then
. The no-interpolation error bound is then
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() entries per zero-crossing, where
entries per zero-crossing, where ![]() is the number of
bits allocated to each table entry.
is the number of
bits allocated to each table entry.
![]() denote the lowpass filter impulse response, and assume it is
twice continuously differentiable for all
denote the lowpass filter impulse response, and assume it is
twice continuously differentiable for all ![]() . By Taylor's theorem
[155, p. 119], we have
. By Taylor's theorem
[155, p. 119], we have
![]() as
as
![$\displaystyle \tilde{h}(t_0+\eta) = \eta\overline{\eta}\left[h^\prime(t_0) -h^\...
...ime\prime}(\xi_0)+\overline{\hat \eta}^{\prime\prime}(\xi_1)
\over 2} \right],
$](img2321.png)
![]() , the maximum curvature of the impulse
response
, the maximum curvature of the impulse
response ![]() , and most lowpass designs will have a value of
, and most lowpass designs will have a value of ![]() very
close to that of the ideal case. The maximum curvature is determined
primarily by the bandwidth of the filter since, generalizing equations
Eq. (I.3.4) and Eq. (I.3.4),
very
close to that of the ideal case. The maximum curvature is determined
primarily by the bandwidth of the filter since, generalizing equations
Eq. (I.3.4) and Eq. (I.3.4),
![]() is approximated by
is approximated by ![]() which is
represented in two's complement fixed-point
arithmetic, then
which is
represented in two's complement fixed-point
arithmetic, then
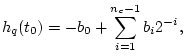
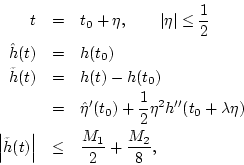
![]() . For the ideal lowpass, we
have
. For the ideal lowpass, we
have