| (2.8) |
As introduced in Book II [452, Appendix G], in the linear,
time-invariant case, a discrete-time state-space model looks
like a vector first-order finite-difference model:
The state-space representation is especially powerful for
multi-input, multi-output (MIMO) linear systems, and also for
time-varying linear systems (in which case any or all of the
matrices in Eq.(1.8) may have time subscripts ![]() ) [221].
) [221].
To cast the previous force-driven mass example in state-space form, we
may first observe that the state of the mass is specified by its
velocity ![]() and position
and position
![]() , or
, or
![]() .2.9Thus, to Eq.(1.5) we may add the explicit difference equation
.2.9Thus, to Eq.(1.5) we may add the explicit difference equation
![$\displaystyle x[(n+1)T] \eqsp x(nT) + T\,v(nT)
\eqsp x(nT) + T\,v[(n-1)T] + \frac{T^2}{m} f[(n-1)T]
$](img253.png)
which, in canonical state-space form, becomes (letting
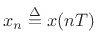 , etc., for notational simplicity)
, etc., for notational simplicity)
General features of this example are that the entire physical state of
the system is collected together into a single vector, and the
elements of the ![]() matrices include physical parameters (and
the sampling interval, in the discrete-time case). The parameters may
also vary with time (time-varying systems), or be functions of the
state (nonlinear systems).
matrices include physical parameters (and
the sampling interval, in the discrete-time case). The parameters may
also vary with time (time-varying systems), or be functions of the
state (nonlinear systems).
The general procedure for building a state-space model is to label all
the state variables and collect them into a vector
![]() , and then
work out the state-transition matrix
, and then
work out the state-transition matrix ![]() , input gains
, input gains ![]() , output
gains
, output
gains ![]() , and any direct coefficient
, and any direct coefficient ![]() . A state variable
. A state variable
![]() is needed for each lumped energy-storage element (mass,
spring, capacitor, inductor), and one for each sample of delay in
sampled distributed systems. After that, various equivalent (but
numerically preferable) forms can be generated by means of
similarity transformations [452, pp. 360-374]. We
will make sparing use of state-space models in this book, because
they can be linear-algebra intensive, and therefore rarely used in
practical real-time signal processing systems for music and audio
effects. However, the state-space framework is an important
general-purpose tool that should be kept in mind [221], and
there is extensive support for state-space models in the matlab
(``matrix laboratory'') language and its libraries. We will use it
mainly as an analytical tool from time to time.
is needed for each lumped energy-storage element (mass,
spring, capacitor, inductor), and one for each sample of delay in
sampled distributed systems. After that, various equivalent (but
numerically preferable) forms can be generated by means of
similarity transformations [452, pp. 360-374]. We
will make sparing use of state-space models in this book, because
they can be linear-algebra intensive, and therefore rarely used in
practical real-time signal processing systems for music and audio
effects. However, the state-space framework is an important
general-purpose tool that should be kept in mind [221], and
there is extensive support for state-space models in the matlab
(``matrix laboratory'') language and its libraries. We will use it
mainly as an analytical tool from time to time.
As noted earlier, a point mass only requires a first-order model:
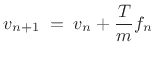
Position