Stability of the FDN is assured when some norm [454] of
the state vector
![]() decreases over time when the input signal is
zero [221, ``Lyapunov stability theory'']. That is, a
sufficient condition for FDN stability is
decreases over time when the input signal is
zero [221, ``Lyapunov stability theory'']. That is, a
sufficient condition for FDN stability is
![$\displaystyle \mathbf{x}(n+1) = \mathbf{A}\left[\begin{array}{c} x_1(n-M_1) \\ [2pt] x_2(n-M_2) \\ [2pt] x_3(n-M_3)\end{array}\right].
$](img567.png)
Using the augmented state-space analysis mentioned above, the inequality of Eq.(2.12) holds under the
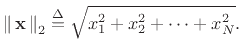
In other words, stability is guaranteed when the feedback matrix decreases the
The matrix norm corresponding to any vector norm
![]() may be defined for the matrix
may be defined for the matrix
![]() as
as
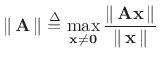
where
It can be shown [168] that the spectral norm of a matrix
![]() is given by the largest singular value of
is given by the largest singular value of
![]() (``
(``
![]() ''), and that this is equal to the
square-root of the largest eigenvalue of
''), and that this is equal to the
square-root of the largest eigenvalue of
![]() , where
, where
![]() denotes the matrix transpose of the real matrix
denotes the matrix transpose of the real matrix
![]() .3.11
.3.11
Since every orthogonal matrix
![]() has spectral norm
1,3.12 a wide variety of stable
feedback matrices can be parametrized as
has spectral norm
1,3.12 a wide variety of stable
feedback matrices can be parametrized as
where
![$\displaystyle {\bm \Gamma}= \left[ \begin{array}{cccc}
g_1 & 0 & \dots & 0\\
0 & g_2 & \dots & 0\\
\vdots & \vdots & \ddots& \vdots\\
0 & 0 & \dots & g_N
\end{array}\right], \quad \left\vert g_i\right\vert<1.
$](img587.png)
An alternative stability proof may be based on showing that an FDN is
a special case of a passive digital waveguide network (derived in
§C.15). This analysis reveals that the FDN is lossless if
and only if the feedback matrix
![]() has unit-modulus eigenvalues
and linearly independent eigenvectors.
has unit-modulus eigenvalues
and linearly independent eigenvectors.