The volume velocity ![]() of a gas flow is defined as particle
velocity
of a gas flow is defined as particle
velocity ![]() times the cross-sectional area
times the cross-sectional area ![]() of the flow, or
of the flow, or
where
When a flow is confined within an enclosed channel, as it is in an
acoustic tube, volume velocity is conserved when the tube
changes cross-sectional area, assuming the density ![]() remains
constant. This follows directly from conservation of mass in a flow:
The total mass passing a given point
remains
constant. This follows directly from conservation of mass in a flow:
The total mass passing a given point ![]() along the flow is given by
the mass density
along the flow is given by
the mass density ![]() times the integral of the volume volume
velocity at that point, or
times the integral of the volume volume
velocity at that point, or
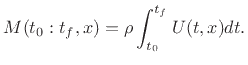
As a simple example, consider a constant flow through two cylindrical
acoustic tube sections having cross-sectional areas ![]() and
and ![]() ,
respectively. If the particle velocity in cylinder 1 is
,
respectively. If the particle velocity in cylinder 1 is ![]() , then
the particle velocity in cylinder 2 may be found by solving
, then
the particle velocity in cylinder 2 may be found by solving
for
It is common in the field of acoustics to denote volume velocity by an
upper-case ![]() . Thus, for the two-cylinder acoustic tube example above,
we would define
. Thus, for the two-cylinder acoustic tube example above,
we would define
![]() and
and
![]() , so that
, so that
would express the conservation of volume velocity from one tube segment to the next.