Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From Eq.(F.1), we have that the general reflectance of impedance
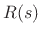 with respect to the reference impedance
with respect to the reference impedance 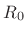 in the wave
variable formulation is given by
in the wave
variable formulation is given by
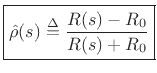 |
(F.10) |
In WDF construction, the free constant in the bilinear transform is taken to be
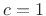 . Thus we obtain
. Thus we obtain
![$ \hat{\rho}_d(z) = \hat{\rho}[(1-z^{-1})/(1+z^{-1})]$](img4849.png) . When
. When
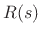 is first order, it is possible to choose the reference
impedance
is first order, it is possible to choose the reference
impedance 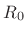 so as to eliminate the delay-free path in the digital
reflectance
so as to eliminate the delay-free path in the digital
reflectance
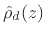 , and so its value depends on the actual
physical element being digitized.
, and so its value depends on the actual
physical element being digitized.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() with respect to the reference impedance
with respect to the reference impedance ![]() in the wave
variable formulation is given by
in the wave
variable formulation is given by