![\includegraphics[width=\twidth]{eps/flstifftstring}](img1443.png) |
An ideal stiff-string synthesis model is drawn in
Fig. 6.13 [10]. See
§C.6 for a detailed derivation. The delay-line length
![]() is the number of samples in
is the number of samples in ![]() periods at frequency
periods at frequency ![]() , where
, where
![]() is the number of the highest partial supported (normally the last
one before
is the number of the highest partial supported (normally the last
one before ![]() ). This is the counterpart of
Fig. 6.12 which depicted ideal-string damping which
was lumped at a single point in the delay-line loop. For the
ideal stiff string, however, (no damping), it is dispersion
filtering that is lumped at a single point of the loop. Dispersion
can be lumped like damping because it, too, is a linear,
time-invariant (LTI) filtering of a propagating wave. Because it is
LTI, dispersion-filtering commutes with other LTI systems in
series, such as delay elements. The allpass filter in
Fig.C.9 corresponds to filter
). This is the counterpart of
Fig. 6.12 which depicted ideal-string damping which
was lumped at a single point in the delay-line loop. For the
ideal stiff string, however, (no damping), it is dispersion
filtering that is lumped at a single point of the loop. Dispersion
can be lumped like damping because it, too, is a linear,
time-invariant (LTI) filtering of a propagating wave. Because it is
LTI, dispersion-filtering commutes with other LTI systems in
series, such as delay elements. The allpass filter in
Fig.C.9 corresponds to filter ![]() in Fig.9.2 for
the Extended Karplus-Strong algorithm. In practice, losses are also
included for realistic string behavior (filter
in Fig.9.2 for
the Extended Karplus-Strong algorithm. In practice, losses are also
included for realistic string behavior (filter ![]() in
Fig.9.2).
in
Fig.9.2).
Allpass filters were introduced in §2.8, and a fairly comprehensive summary is given in Book II of this series [452, Appendix C].7.8The general transfer function for an allpass filter is given (in the real, single-input, single-output case) by
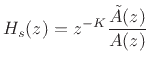
where
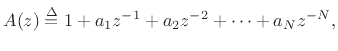
and
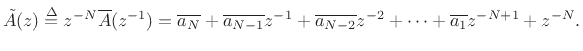
We may think of
Section 6.11 below discusses some
methods for designing stiffness allpass filters ![]() from
measurements of stiff vibrating strings, and
§9.4.1 gives further details for the case of piano
string modeling.
from
measurements of stiff vibrating strings, and
§9.4.1 gives further details for the case of piano
string modeling.