The rotational version of Newton's law ![]() is
is
![\begin{eqnarray*}
\tau &=& \dot{L} \,\eqss \, I\dot{\omega}\,\isdefss \, I\alpha\\ [5pt]
f &=& \dot{p} \,\eqss \, m\dot{v}\,\isdefss \, ma
\end{eqnarray*}](img2954.png)
To show that Eq.(B.28) results from Newton's second law ![]() ,
consider again a mass
,
consider again a mass ![]() rotating at a distance
rotating at a distance ![]() from an axis
of rotation, as in §B.4.3 above, and
let
from an axis
of rotation, as in §B.4.3 above, and
let ![]() denote a tangential force on the mass, and
denote a tangential force on the mass, and ![]() the corresponding tangential acceleration. Then we have, by Newton's
second law,
the corresponding tangential acceleration. Then we have, by Newton's
second law,
Multiplying both sides by
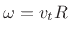
where we used the definitions
from Newton's second law
In summary, force equals the time-derivative of linear momentum, and torque equals the time-derivative of angular momentum. By Newton's laws, the time-derivative of linear momentum is mass times acceleration, and the time-derivative of angular momentum is the mass moment of inertia times angular acceleration: