In the uniformly sampled case (![]() for some sampling interval
for some sampling interval
![]() ), a Lagrange interpolator can be viewed as a Finite Impulse
Response (FIR) filter [452]. Such filters are often called
fractional delay filters
[269], since they are filters providing a non-integer time delay, in general.
Let
), a Lagrange interpolator can be viewed as a Finite Impulse
Response (FIR) filter [452]. Such filters are often called
fractional delay filters
[269], since they are filters providing a non-integer time delay, in general.
Let ![]() denote the impulse response of such a
fractional-delay filter. That is, assume the interpolation at point
denote the impulse response of such a
fractional-delay filter. That is, assume the interpolation at point
![]() is given by
is given by
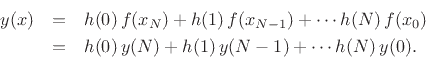
where we have set ![]() for simplicity, and used the fact that
for simplicity, and used the fact that
![]() for
for
![]() in the case of ``true
interpolators'' that pass through the given samples exactly. For best
results,
in the case of ``true
interpolators'' that pass through the given samples exactly. For best
results, ![]() should be evaluated in a one-sample range centered
about
should be evaluated in a one-sample range centered
about ![]() . For delays outside the central one-sample range, the
coefficients can be shifted to translate the desired delay into
that range.
. For delays outside the central one-sample range, the
coefficients can be shifted to translate the desired delay into
that range.