Viewing Eq.(7.2) in the frequency domain, the ideal
differentiator transfer-function is ![]() , which can be viewed as
the Laplace transform of the operator
, which can be viewed as
the Laplace transform of the operator ![]() (left-hand side of
Eq.(7.2)). Moving to the right-hand side, the z transform of the
first-order difference operator is
(left-hand side of
Eq.(7.2)). Moving to the right-hand side, the z transform of the
first-order difference operator is
![]() . Thus, in the
frequency domain, the finite-difference approximation may be performed
by making the substitution
. Thus, in the
frequency domain, the finite-difference approximation may be performed
by making the substitution
The inverse of substitution Eq.(7.3) is
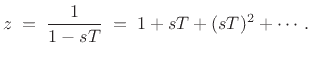
As discussed in §8.3.1, the FDA is a special case of the
matched ![]() transformation applied to the point
transformation applied to the point ![]() .
.
Note that the FDA does not alias, since the conformal mapping
![]() is one to one. However, it does warp the poles and zeros in a
way which may not be desirable, as discussed further on p.
is one to one. However, it does warp the poles and zeros in a
way which may not be desirable, as discussed further on p. ![]() below.
below.