A finite-difference scheme is said to be
consistent with the original
partial differential equation if, given any sufficiently
differentiable function ![]() , the differential equation operating
on
, the differential equation operating
on ![]() approaches the value of the finite difference equation
operating on
approaches the value of the finite difference equation
operating on ![]() , as
, as ![]() and
and ![]() approach zero.
approach zero.
Thus, in the ideal string example, to show the consistency of Eq.(D.3) we must show that
![$\displaystyle \left(\frac{\partial^2}{\partial x^2}
- \frac{1}{c^2}
\frac{\partial^2}{\partial t^2} \right)y(t,x)
= \lim_{T,X\to0}
\left[
(\delta_x + \delta_x^{-1})
-
(\delta_t + \delta_t^{-1})
\right] y_{n,m}
$](img4524.png)
for all
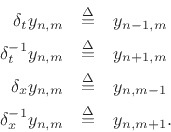
In taking the limit as ![]() and
and ![]() approach zero, we must maintain
the relationship
approach zero, we must maintain
the relationship ![]() , and we must scale the FDS by
, and we must scale the FDS by ![]() in
order to achieve an exact result:
in
order to achieve an exact result:
![\begin{eqnarray*}
\lefteqn{\lim_{T,X\to0}
\frac{1}{X^2}
\left[
(\delta_x + \delta_x^{-1})
-
(\delta_t + \delta_t^{-1})
\right] y_{n,m}} \qquad\qquad& &\\
&=&
\lim_{T,X\to0}
\left[
\frac{\delta_x + 2 + \delta_x^{-1}}{X^2}
-
\frac{\delta_t + 2 + \delta_t^{-1}}{c^2T^2}
\right] y_{n,m}\\
&\isdef & \left(\frac{\partial^2}{\partial x^2}
- \frac{1}{c^2}
\frac{\partial^2}{\partial t^2} \right)y(t,x)
\end{eqnarray*}](img4531.png)
as required. Thus, the FDS is consistent. See, e.g., [484] for more examples.
In summary, consistency of a finite-difference scheme means that, in the limit as the sampling intervals approach zero, the original PDE is obtained from the FDS.