Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Computation of the STFT consists of the following steps:
1. Read 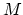 samples of the input signal
samples of the input signal 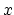 into a local buffer,
into a local buffer,
where 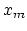 is called the
is called the  th frame of the input signal,
and
th frame of the input signal,
and
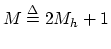 is the frame length (which we assume is odd
for reasons to be discussed later). The time advance
is the frame length (which we assume is odd
for reasons to be discussed later). The time advance 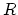 (in
samples) from one frame to the next is called the hop size.
(in
samples) from one frame to the next is called the hop size.
2. Multiply the data frame pointwise by a length 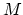 spectrum analysis
window
spectrum analysis
window
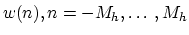 to obtain the
to obtain the  th windowed data
frame:
th windowed data
frame:
3. Extend
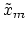 with zeros on both sides to obtain a zero-padded
windowed data frame:
with zeros on both sides to obtain a zero-padded
windowed data frame:
where 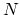 is the FFT size, chosen to be
a power of two larger than
is the FFT size, chosen to be
a power of two larger than 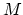 . The number
. The number
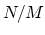 is called the zero-padding factor.
is called the zero-padding factor.
4. Take a length 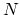 FFT of
FFT of
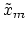 to obtain the STFT at time
to obtain the STFT at time  :
:
where
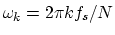 , and
, and 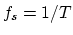 is the sampling rate in
Hz. The STFT bin number is
is the sampling rate in
Hz. The STFT bin number is 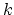 . Each bin
. Each bin
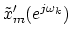 of
the STFT can be regarded as a sample of the complex signal at the
output of a lowpass filter whose input is
of
the STFT can be regarded as a sample of the complex signal at the
output of a lowpass filter whose input is
 ;
this signal is
;
this signal is
 frequency-shifted so that frequency
frequency-shifted so that frequency  is
moved to 0 Hz. In this interpretation, the hop size
is
moved to 0 Hz. In this interpretation, the hop size 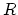 is the downsampling factor applied to each bandpass output, and the
analysis window
is the downsampling factor applied to each bandpass output, and the
analysis window
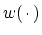 is the impulse response of the
anti-aliasing filter used with the downsampling.
is the impulse response of the
anti-aliasing filter used with the downsampling.
The zero-padding factor is the interpolation factor for the
spectrum, i.e., each FFT bin is replaced by 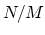 bins, interpolating
the spectrum.
bins, interpolating
the spectrum.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download parshl.pdf
![]() samples of the input signal
samples of the input signal ![]() into a local buffer,
into a local buffer,
![]() spectrum analysis
window
spectrum analysis
window
![]() to obtain the
to obtain the ![]() th windowed data
frame:
th windowed data
frame:
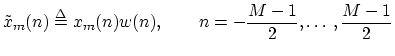
![]() with zeros on both sides to obtain a zero-padded
windowed data frame:
with zeros on both sides to obtain a zero-padded
windowed data frame:
![$\displaystyle \tilde{x}_m^\prime (n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}\le...
...}-1 \\ [5pt]
0, & -\frac{N}{2}\leq n < -{\frac{M-1}{2}} \\
\end{array}\right.
$](img11.png)
![]() FFT of
FFT of
![]() to obtain the STFT at time
to obtain the STFT at time ![]() :
:
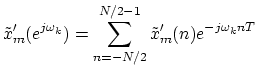
![]() bins, interpolating
the spectrum.
bins, interpolating
the spectrum.