To obtain oscillator-control envelopes for additive synthesis, the
amplitude, frequency, and phase trajectories are estimated once per
FFT hop by the STFT. It is customary in computer music to linearly interpolate the amplitude and frequency trajectories from
one hop to the next. Call these signals
![]() and
and
![]() ,
defined now for all
,
defined now for all ![]() at the normal signal sampling rate. The phase
is usually discarded at this stage and redefined as the integral of
the instantaneous frequency when needed:
at the normal signal sampling rate. The phase
is usually discarded at this stage and redefined as the integral of
the instantaneous frequency when needed:
![]() . When phase must be matched in a given frame, the
frequency can instead move quadratically across the frame to provide
cubic polynomial phase interpolation [12], or a
second linear breakpoint can be introduced somewhere in the frame for
the frequency trajectory.
. When phase must be matched in a given frame, the
frequency can instead move quadratically across the frame to provide
cubic polynomial phase interpolation [12], or a
second linear breakpoint can be introduced somewhere in the frame for
the frequency trajectory.
6. Apply any desired modification to the analysis data, such as time scaling, pitch transposition, formant modification, etc.
7. Use the (possibly modified) amplitude and frequency trajectories to control a summing oscillator bank:
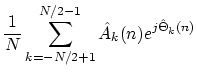 |
(4) | ||
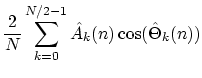 |
(5) |