Nonlinear Commuted Model

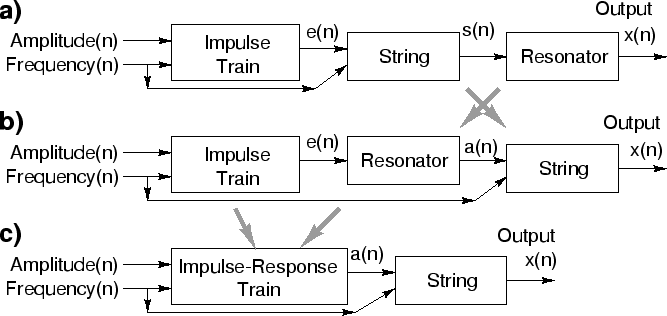
The basic idea of commuted synthesis is to interchange the order of implementation of the string and the body resonator, as depicted in Fig. 1.

Figure: a) Simplified bowed string model, including only amplitude, pitch, and vibrato control capability. b) Equivalent diagram with resonator and string commuted. c) Equivalent diagram in which the resonator impulse response is played into the string each pitch period.

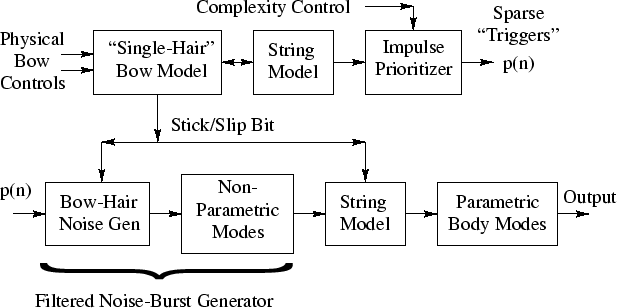
The bowed string synthesizer of the present paper is shown in Fig. 2. The bottom half is Fig. 1c, with an external trigger input, and some further details regarding pulsed noise generation. The top half of Fig. 2 provides an explicit model of bow-string dynamics. The ``Impulse Prioritizer'' measures the timing and amplitude of the largest impulses in the string waveform at the bridge and passes on the most important ones subject to complexity constraints. The second string which is driven by the BIR oscillators may be a digital waveguide model driven at the bowing point, or it may consist of an equivalent feedforward comb filter followed by a filtered delay loop. However, the advantage of a a full waveguide model of the string [11] is that the time-varying, nonlinear, partial termination of the string by the bow can be more conveniently implemented.

The Stick/Slip Bit can be used to switch between two models of partial string termination by the bow. For more accurate control of string damping by the bow, the contact force, relative velocity, position along the string, and bow angle can all be used to determine the frequency-dependent scattering junction created by the bow on the string [11]. It was found empirically that significant damping of the string by the bow is necessary for obtaining robust Helmholtz motion; otherwise, excessive ringing of the string segment between the bow and nut tends to cause slipping at times disruptive to the Helmholtz motion. Intuitively, one of the two ``Helmholtz corners'' sent in opposite directions along the string on each slip/stick impulse must be ``filtered out'' by the bow, while the other is ``amplified'' by the stick/slip process. Graphical animation of the bowed string motion was found to be very helpful for determining qualitative factors such as this.

Figure: Commuted bowed string synthesis model driven by a separate bow-string model exhibiting full nonlinear dynamic behavior.