Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
It is common terminology to call
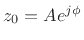 the complex sinusoid's
phasor (or ``phase vector''), and
the complex sinusoid's
phasor (or ``phase vector''), and
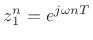 its carrier wave.
its carrier wave.
For a real sinusoid,
the phasor is again defined as
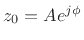 and the carrier is
and the carrier is
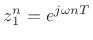 . However, in this case, the real sinusoid
is recovered from its complex-sinusoid counterpart by taking the real part:
. However, in this case, the real sinusoid
is recovered from its complex-sinusoid counterpart by taking the real part:
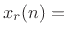
re
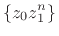
The phasor magnitude
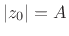 is the
amplitude of the sinusoid.
The phasor angle
is the
amplitude of the sinusoid.
The phasor angle
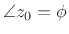 is the
phase of the sinusoid.
is the
phase of the sinusoid.
When working with complex sinusoids, as in Eq.(4.11), the phasor
representation
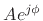 of a sinusoid can be thought of as simply the
complex amplitude of the sinusoid. I.e.,
it is the complex constant that multiplies the carrier term
of a sinusoid can be thought of as simply the
complex amplitude of the sinusoid. I.e.,
it is the complex constant that multiplies the carrier term
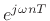 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
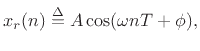
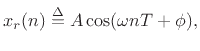
![]() of a sinusoid can be thought of as simply the
complex amplitude of the sinusoid. I.e.,
it is the complex constant that multiplies the carrier term
of a sinusoid can be thought of as simply the
complex amplitude of the sinusoid. I.e.,
it is the complex constant that multiplies the carrier term
![]() .
.