Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Going back to our simple 2D example ![$ x=[2, 3]$](img745.png) ,
we can compute its norm as
,
we can compute its norm as
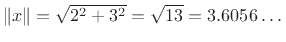 .
The physical interpretation of the norm as a distance measure
is shown in Fig.5.5.
.
The physical interpretation of the norm as a distance measure
is shown in Fig.5.5.
Figure 5.5:
Geometric interpretation of a
signal norm in 2D.
![\includegraphics[scale=0.7]{eps/vec2dlen}](img747.png) |
Figure 5.6:
Length of vectors in sum.
![\includegraphics[scale=0.7]{eps/vecsumdist}](img748.png) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[scale=0.7]{eps/vec2dlen}](img747.png)