Our second extended example is a boundary value problem for Laplace's equation. The underlying physical problem involves the conductivity of a medium with cylindrical inclusions and is considered by Keller and Sachs [7].
Find a function ![]() satisfying Laplace's equation
satisfying Laplace's equation
u = 0
n
-------------
| .
| .
| .
| . u = 1
| .
| .
| .
u = 0 | |
| |
| |
| | u = 1
| |
| |
| |
------------------------
u = 0
n
The effective conductivity of an medium is then given by the
integral along the left edge,
Keller and Sachs use a finite difference approximation. The following technique makes use of the fact that the equation is actually Laplace's equation and leads to a much smaller matrix problem to solve.
Consider an approximate solution of the form

The computational task is to find coefficients so that the
boundary conditions on the remaining edges are satisfied as well
as possible. To accomplish this, pick m points (r,t) on the
remaining edges. It is desirable to have m > n and in practice
we usually choose m to be two or three times as large as n .
Typical values of n are 10 or 20 and of m are 20 to 60. An
m by n matrix A is generated. The i,j element is the j-th
basis function, or its normal derivative, evaluated at the i-th
boundary point. A right hand side with m components is also
generated. In this example, the elements of the right hand side
are either zero or one. The coefficients are then found by
solving the overdetermined set of equations
Once the coefficients have been determined, the approximate
solution is defined everywhere on the domain. It is then
possible to compute the effective conductivity sigma . In fact,
a very simple formula results,
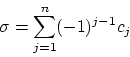
//Conductivity example.
//Parameters ---
rho //radius of cylindrical inclusion
n //number of terms in solution
m //number of boundary points
//initialize operation counter
flop = <0 0>;
//initialize variables
m1 = round(m/3); //number of points on each straight edge
m2 = m - m1; //number of points with Dirichlet conditions
pi = 4*atan(1);
//generate points in Cartesian coordinates
//right hand edge
for i = 1:m1, x(i) = 1; y(i) = (1-rho)*(i-1)/(m1-1);
//top edge
for i = m2+1:m, x(i) = (1-rho)*(m-i)/(m-m2-1); y(i) = 1;
//circular edge
for i = m1+1:m2, t = pi/2*(i-m1)/(m2-m1+1); ...
x(i) = 1-rho*sin(t); y(i) = 1-rho*cos(t);
//convert to polar coordinates
for i = 1:m-1, th(i) = atan(y(i)/x(i)); ...
r(i) = sqrt(x(i)**2+y(i)**2);
th(m) = pi/2; r(m) = 1;
//generate matrix
//Dirichlet conditions
for i = 1:m2, for j = 1:n, k = 2*j-1; ...
a(i,j) = r(i)**k*cos(k*th(i));
//Neumann conditions
for i = m2+1:m, for j = 1:n, k = 2*j-1; ...
a(i,j) = k*r(i)**(k-1)*sin((k-1)*th(i));
//generate right hand side
for i = 1:m2, b(i) = 1;
for i = m2+1:m, b(i) = 0;
//solve for coefficients
c = A\b
//compute effective conductivity
c(2:2:n) = -c(2:2:n);
sigma = sum(c)
//output total operation count
ops = flop(2)
The program can be used within MATLAB by setting the three parameters and then accessing the file. For example,
rho = .9;
n = 15;
m = 30;
exec('PDE')
The resulting output is
RHO =
.9000
N =
15.
M =
30.
C =
2.2275
-2.2724
1.1448
0.1455
-0.1678
-0.0005
-0.3785
0.2299
0.3228
-0.2242
-0.1311
0.0924
0.0310
-0.0154
-0.0038
SIGM =
5.0895
OPS =
16204.
A total of 16204 floating point operations were necessary to set up the matrix, solve for the coefficients and compute the conductivity. The operation count is roughly proportional to m*n**2. The results obtained for sigma as a function of rho by this approach are essentially the same as those obtained by the finite difference technique of Keller and Sachs, but the computational effort involved is much less.