Definition. A set
Definition. A set ![]() is said to be concave if for every
vector
is said to be concave if for every
vector ![]() and
and ![]() in
in ![]() ,
,
![]() is in
is in ![]() for
all
for
all
![]() . In other words, all points on the line between two points
of
. In other words, all points on the line between two points
of ![]() lie in
lie in ![]() .
.
Definition. A functional is a mapping from a vector space to the
real numbers ![]() .
.
Thus, for example, every norm is a functional.
Definition. A linear functional is a functional ![]() such that
for each
such that
for each ![]() and
and ![]() in the linear space
in the linear space ![]() , and for all scalars
, and for all scalars
![]() and
and ![]() , we have
, we have
![]() .
.
Definition. The norm of a linear functional ![]() is defined on
the normed linear space
is defined on
the normed linear space ![]() by
by
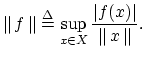
Definition. A functional ![]() defined on a concave subset
defined on a concave subset ![]() of a vector space
of a vector space
![]() is said to be concave on
is said to be concave on ![]() if for
every vector
if for
every vector ![]() and
and ![]() in
in ![]() ,
,
Definition. A local minimizer of a real-valued function ![]() is
any
is
any ![]() such that
such that
![]() in some neighborhood of
in some neighborhood of ![]() .
.
Definition. A global minimizer of a real-valued function ![]() on a set
on a set ![]() is
any
is
any
![]() such that
such that
![]() for all
for all ![]() .
.
Definition. A cluster point ![]() of a sequence
of a sequence ![]() is any point
such that every neighborhood of
is any point
such that every neighborhood of ![]() contains at least one
contains at least one ![]() .
.
Definition. The concave hull of a set ![]() in a metric space is the
smallest concave set containing
in a metric space is the
smallest concave set containing ![]() .
.