Parallel Junction of Multivariable Complex Waveguides

We now consider the scattering matrix for the parallel junction of $N$ $m$-variable physical waveguides, and at the same time, we treat the generalized case of matrix transfer-function wave impedances. Equations (21) and (16) can be rewritten for each $m$-variable branch as

$$\begin{array}{rcr} {\mbox{\boldmath$u$}}_i^+ &=& {\mbox{\bol... ...\Gamma$}}^{*}_i(1/z^*){\mbox{\boldmath$p$}}_i^- \,, \end{array}$$ (58)

and

$$\begin{array}{l} {\mbox{\boldmath$u$}}_i = {\mbox{\boldmath$... ...ldmath$p$}}_i^- = p_{\rm J}{\mbox{\boldmath$1$}}\,, \end{array}$$ (59)

where ${\mbox{\boldmath$\Gamma$}}_i(z)={\mbox{\boldmath$R$}}_i^{-1}(z)$, $p_{\rm J}$ is the pressure at the junction, and we have used pressure continuity to equate ${\mbox{\boldmath$p$}}_i$ to $p_{\rm J}$ for any $i$.

Using conservation of velocity we obtain

$$0 = {\mbox{\boldmath$1$}}^T{\sum_{i=1}^{N}{{\mbox{\boldmath$u$}}_i}}$$

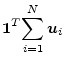$$= {\mbox{\boldmath$1$}}^T{\displaystyle \sum_{i=1}^{N}}\left\{\left... ...{\mbox{\boldmath$\Gamma$}}^{*}_i(1/z^*)\right]{\mbox{\boldmath$p$}}_i^+ \right.$$

$$\left. \qquad - {\mbox{\boldmath$\Gamma$}}^{*}_i(1/z^*)p_{\rm J}{\mbox{\boldmath$1$}}\right\}$$ (60)

and

$$p_{\rm J}= S {\mbox{\boldmath$1$}}^T {\sum_{i=1}^{N}{\left[{... ...$\Gamma$}}^{*}_i(1/z^*)\right] {\mbox{\boldmath$p$}}_i^+}} \,,$$ (61)

where

$$S = \left\{{\mbox{\boldmath$1$}}^T\left[{\sum_{i=1}^{N}{{\mb... ...}}^{*}_i(1/z^*)}}\right]{\mbox{\boldmath$1$}}\right\}^{-1} \,.$$ (62)

From (57), we have the scattering relation

$${\mbox{\boldmath$p$}}^- = \left[ \begin{array}{l} {\mbox{\boldmath$p$}}_1^- \\ \vdots \\ ... ...ath$p$}}_N^- \end{array} \right] = {\mbox{\boldmath$A$}}{\mbox{\boldmath$p$}}^+$$

$$= {\mbox{\boldmath$A$}}\left[ \begin{array}{l} {\mbox{\boldmath$p$}... ...array}{l} 1 \\ \vdots \\ 1 \end{array} \right] - {\mbox{\boldmath$p$}}^+ \: ,$$ (63)

where the scattering matrix is deduced from (59):

$${\mbox{\boldmath$A$}}= S \left[\begin{array}{l}{\mbox{\boldm... ...d{array} \right] \end{array}\right] - {\mbox{\boldmath$I$}}\,.$$ (64)

If the branches do not all have the same dimensionality $m$, we may still use the expression (62) by letting $m$ be the largest dimensionality and embedding each branch in an $m$-variable propagation space.